题目内容
(1)填空:(a-1)(a+1)= (a-1)(a2+a+1)= (a-1)(a3+a2+a+1)= (2)你发现规律了吗?请你用你发现的规律填空:(a-1)(an+an-1+…+a2+a+1)=
(3)根据上述规律,请你求42012+42011+42010+…+4+1的值. .
(3)根据上述规律,请你求42012+42011+42010+…+4+1的值.
考点:多项式乘多项式
专题:规律型
分析:(1)根据平方差公式和立方差公式可得前2个式子的结果,利用多项式乘以多项式的方法可得出第3个式子的结果;
(2)从而总结出规律是:(a-1)(an+an-1+…+a2+a+1)=an+1-1;
(3)根据上述结论计算下列式子即可.
(2)从而总结出规律是:(a-1)(an+an-1+…+a2+a+1)=an+1-1;
(3)根据上述结论计算下列式子即可.
解答:解:根据题意:(1)(a-1)(a+1)=a2-1;
(a-1)(a2+a+1)=a3-1;
(a-1)(a3+a2+a+1)=a4-1;
(2)(a-1)(an+an-1+an-2+…+a2+a+1)=an+1-1.
(3)根据以上分析(1)42012+42011+42010+…+4+1299+298+297+…+4+1,
=
(4-1)(42012+42011+42010+…+4+1),
=
(42013-1).
故答案为:(1)a2-1,a3-1,a4-1;(2)an+1-1;(3)
(42013-1).
(a-1)(a2+a+1)=a3-1;
(a-1)(a3+a2+a+1)=a4-1;
(2)(a-1)(an+an-1+an-2+…+a2+a+1)=an+1-1.
(3)根据以上分析(1)42012+42011+42010+…+4+1299+298+297+…+4+1,
=
| 1 |
| 3 |
=
| 1 |
| 3 |
故答案为:(1)a2-1,a3-1,a4-1;(2)an+1-1;(3)
| 1 |
| 3 |
点评:主要考查了学生的分析、总结、归纳能力,规律型的习题一般是从所给的数据和运算方法进行分析,从特殊值的规律上总结出一般性的规律.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
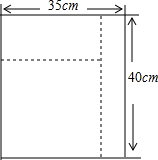 如图所示,有一块长为40cm、宽为35cm的长方形红布,晶晶的妈妈想把它剪成一个正方形,第一次她剪去了一个一定宽度的长方形布片,然后在剩下的长方形布片中又剪去长方形的布片,这次剪去的布片的宽度是上次的2倍,这样剩下的布片恰好是一个正方形,请问晶晶妈妈第一次剪去的长方形布片的宽为多少厘米?
如图所示,有一块长为40cm、宽为35cm的长方形红布,晶晶的妈妈想把它剪成一个正方形,第一次她剪去了一个一定宽度的长方形布片,然后在剩下的长方形布片中又剪去长方形的布片,这次剪去的布片的宽度是上次的2倍,这样剩下的布片恰好是一个正方形,请问晶晶妈妈第一次剪去的长方形布片的宽为多少厘米?