题目内容
13.若原点O与反比例函数y=$\frac{k}{x}$(k<0)的图象上的点之间的距离的最小值为4,则k的值为8.分析 根据反比例函数图象上点的坐标特征、点到原点的距离公式得到关于k的方程组;根据方程组,求得k的值.
解答 解:设y=$\frac{k}{x}$(k>0)的图象上的距离原点最近的点为P(x,$\frac{k}{x}$),
则d=$\sqrt{{x}^{2}+(\frac{k}{x})^{2}}$=4,
∵x2+($\frac{k}{x}$)2≥2x•=$\frac{k}{x}$=16,即16=2k,
∴k=8,
故答案为8.
点评 本题考查了反比例函数图象上点的坐标特征.解题时把反比例函数y=$\frac{k}{x}$的图象、两点之间距离公式相结合,考查了学生对所学知识的综合运用能力.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
3.小强的年龄比妈妈小33岁,今年妈妈的年龄正好是小强的4倍,小强今年的年龄是( )
| A. | 10岁 | B. | 11岁 | C. | 12岁 | D. | 13岁 |
18.某学校报告厅的一部分为扇形,观众席的座位设置如下表:
则每排的座位数m与排数n的关系式为m=3n+35.
| 排数n | 1 | 2 | 3 | 4 | … |
| 座位数m | 38 | 41 | 44 | 47 | … |
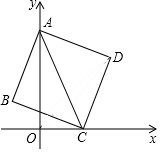 如图,在平面直角坐标系中,边长为2的正方形ABCD的顶点A落在y轴上,点C落在x轴上,随着顶点C中原点O向x轴的正半轴方向移动,顶点A也沿y轴的负半轴方向运动到O,当顶点A和原点O重合时,顶点D的坐标为($\sqrt{2}$,$\sqrt{2}$),在整个运动过程中,点D的移动长度是4$\sqrt{2}$-4.
如图,在平面直角坐标系中,边长为2的正方形ABCD的顶点A落在y轴上,点C落在x轴上,随着顶点C中原点O向x轴的正半轴方向移动,顶点A也沿y轴的负半轴方向运动到O,当顶点A和原点O重合时,顶点D的坐标为($\sqrt{2}$,$\sqrt{2}$),在整个运动过程中,点D的移动长度是4$\sqrt{2}$-4. 已知等边△ABC,E为平面内任意点,连接AE,将线段AE绕点A顺时针旋转60°得到AD,连接BD,CE.
已知等边△ABC,E为平面内任意点,连接AE,将线段AE绕点A顺时针旋转60°得到AD,连接BD,CE.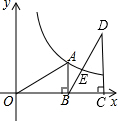 如图,双曲线y=$\frac{k}{x}$上有一点A,过A作AB⊥x轴于B,已知OB=3,△AOB≌△BDC,若反比例函数图象恰好经过BD的中点E,则k的值为( )
如图,双曲线y=$\frac{k}{x}$上有一点A,过A作AB⊥x轴于B,已知OB=3,△AOB≌△BDC,若反比例函数图象恰好经过BD的中点E,则k的值为( )