题目内容
1.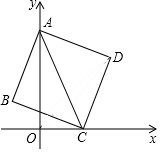 如图,在平面直角坐标系中,边长为2的正方形ABCD的顶点A落在y轴上,点C落在x轴上,随着顶点C中原点O向x轴的正半轴方向移动,顶点A也沿y轴的负半轴方向运动到O,当顶点A和原点O重合时,顶点D的坐标为($\sqrt{2}$,$\sqrt{2}$),在整个运动过程中,点D的移动长度是4$\sqrt{2}$-4.
如图,在平面直角坐标系中,边长为2的正方形ABCD的顶点A落在y轴上,点C落在x轴上,随着顶点C中原点O向x轴的正半轴方向移动,顶点A也沿y轴的负半轴方向运动到O,当顶点A和原点O重合时,顶点D的坐标为($\sqrt{2}$,$\sqrt{2}$),在整个运动过程中,点D的移动长度是4$\sqrt{2}$-4.
分析 如图1中,顶点A和原点O重合时,作DH⊥OC于H.利用等腰三角形的性质即可解决问题.如图2中,作DE⊥OA于E,DF⊥OC于F,取AC中点H,连接OH,DH.首先证明点D在∠AOC的平分线上运动,求出OD的最大值、最小值,再判断点D的运动路径即可解决问题.
解答 解:如图1中,顶点A和原点O重合时,作DH⊥OC于H.
∵AC=2$\sqrt{2}$,△ADC是等腰直角三角形,
∴DH=OH=$\sqrt{2}$,
∴D($\sqrt{2}$,$\sqrt{2}$),
如图2中,作DE⊥OA于E,DF⊥OC于F,取AC中点H,连接OH,DH.
∵∠ADC=∠EDF=90°,
∴∠ADE=∠CDF,
∵DA=DC,∠DEA=∠DFC,
∴△DEA≌△DFC,
∴DE=DF,
∵DE⊥OA于E,DF⊥OC于F,
∴∠DOE=∠DOF=45°,
∴点D在∠AOC的平分线上运动,
∵OD≤DH+OH,
∴OD≤2$\sqrt{2}$,
∴OD的最大值为2$\sqrt{2}$,
当A与O重合时,OD的值最小,最小值为2,当C与O重合时,OD的值最小,最小值为2,
观察图象可知,OD的值逐渐增大然后逐渐减小,
∴点D的移动长度=2(2$\sqrt{2}$-2)=4$\sqrt{2}$-4,
故答案为($\sqrt{2}$,$\sqrt{2}$),4$\sqrt{2}$-4.
点评 本题考查了正方形的性质(四边相等,四角相等,对角线互相垂直平分,且平分每一组对角)以及坐标与图形的性质,全等三角形的判定和性质,解直角三角形,勾股定理的运用,三角形的三边关系的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.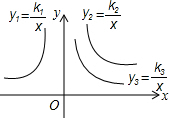 如图,是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
如图,是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
 如图,是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
如图,是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )| A. | k1>k2>k3 | B. | k3>k1>k2 | C. | k2>k3>k1 | D. | k3>k2>k1 |
10.在实数$\sqrt{196}$,-π,$\frac{1}{3}$,0.010010001中,无理数是( )
| A. | $\sqrt{196}$ | B. | -π | C. | $\frac{1}{3}$ | D. | 0.010010001 |

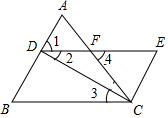 填空,并在括号内填写理由.
填空,并在括号内填写理由. 快车与慢车分别从甲、乙两地同时出发,匀速相向而行,快车到达乙地后立刻返回,慢车到达甲地后停止行驶.途中折线表示从两车出发到慢车到达甲地过程中,两车间的距离y(km)与慢车行驶时间x(h)之间的函数关系,根据图中信息,有下列说法:①甲、乙两地相距400km;②快车速度是慢车速度的1.5倍;③快车从甲地到乙地共用了$\frac{10}{3}$小时;④点A的坐标为(5,200);其中符合图象描述的说法有( )
快车与慢车分别从甲、乙两地同时出发,匀速相向而行,快车到达乙地后立刻返回,慢车到达甲地后停止行驶.途中折线表示从两车出发到慢车到达甲地过程中,两车间的距离y(km)与慢车行驶时间x(h)之间的函数关系,根据图中信息,有下列说法:①甲、乙两地相距400km;②快车速度是慢车速度的1.5倍;③快车从甲地到乙地共用了$\frac{10}{3}$小时;④点A的坐标为(5,200);其中符合图象描述的说法有( )