题目内容
2.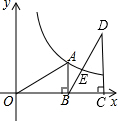 如图,双曲线y=$\frac{k}{x}$上有一点A,过A作AB⊥x轴于B,已知OB=3,△AOB≌△BDC,若反比例函数图象恰好经过BD的中点E,则k的值为( )
如图,双曲线y=$\frac{k}{x}$上有一点A,过A作AB⊥x轴于B,已知OB=3,△AOB≌△BDC,若反比例函数图象恰好经过BD的中点E,则k的值为( )| A. | 1 | B. | 3 | C. | 6 | D. | 9 |
分析 过E作EF⊥BD于F,于是得到EF∥CD得到$\frac{BE}{ED}$=$\frac{BF}{FC}$,根据E是BD的中点,得到BF=FC,EF=$\frac{1}{2}$DC,设AB=a,根据全等三角形的性质得到BC=a,CD=OB=3,于是得到D(3+a,3),A(3,a),根据反比例函数图象上点的坐标特征即可得到结论.
解答 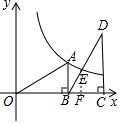 解:过E作EF⊥BD于F,则EF∥CD,
解:过E作EF⊥BD于F,则EF∥CD,
∴$\frac{BE}{ED}$=$\frac{BF}{FC}$,
∵E是BD的中点,
∴BF=FC,EF=$\frac{1}{2}$DC,
设AB=a,
∵OB=3,△AOB≌△BDC,
∴BC=a,CD=OB=3,
D(3+a,3),A(3,a),
∴反比例函数的解析式为y=$\frac{3a}{x}$,
∴E(3+$\frac{a}{2}$,$\frac{3}{2}$),
∵反比例函数图象点E,
∴(3+$\frac{a}{2}$)$\frac{3}{2}$=3a,
∵解得:a=2,
∴3a=6,
∴k=3a=6,
故选C.
点评 本题考查了反比例函数图象上点的坐标特征,全等三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
12.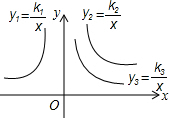 如图,是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
如图,是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
 如图,是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
如图,是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )| A. | k1>k2>k3 | B. | k3>k1>k2 | C. | k2>k3>k1 | D. | k3>k2>k1 |
10.在实数$\sqrt{196}$,-π,$\frac{1}{3}$,0.010010001中,无理数是( )
| A. | $\sqrt{196}$ | B. | -π | C. | $\frac{1}{3}$ | D. | 0.010010001 |
 如图所示,?ABCD的顶点A、D在反比例函数$y=\frac{k}{x}$(k<0,x<0)的图象上,顶点B、C分别在坐标轴上.
如图所示,?ABCD的顶点A、D在反比例函数$y=\frac{k}{x}$(k<0,x<0)的图象上,顶点B、C分别在坐标轴上. 如图,为了解全班同学对“告别六一”活动的三种方案的意见,七年级某班班委会作了一次全面调查,得到扇形图,若调查结果知,赞成甲方案的有10人,弃权的有6人,则赞成丙方案的有14人.
如图,为了解全班同学对“告别六一”活动的三种方案的意见,七年级某班班委会作了一次全面调查,得到扇形图,若调查结果知,赞成甲方案的有10人,弃权的有6人,则赞成丙方案的有14人.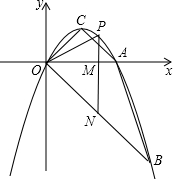 如图,抛物线y=ax2+bx经过A(2,0),B(3,-3)两点,抛物线的顶点为C,动点P在直线OB上方的抛物线上,过点P作直线PM∥y轴,交x轴于M,交OB于N,设点P的横坐标为m.
如图,抛物线y=ax2+bx经过A(2,0),B(3,-3)两点,抛物线的顶点为C,动点P在直线OB上方的抛物线上,过点P作直线PM∥y轴,交x轴于M,交OB于N,设点P的横坐标为m.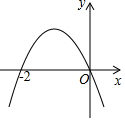 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①抛物线的对称轴为x=-1;②abc=0;③方程ax2+bx+c+1=0有两个不相等的实数根;④无论x取何值,ax2+bx≤a-b.其中,正确的个数为( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①抛物线的对称轴为x=-1;②abc=0;③方程ax2+bx+c+1=0有两个不相等的实数根;④无论x取何值,ax2+bx≤a-b.其中,正确的个数为( )