��Ŀ����
����Ŀ���Ķ�������ϣ���ɺ�����Ŀ��
0��-360����Ľǵ����Ǻ���
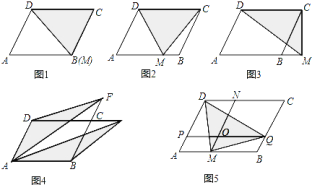
�ڳ��У�����ѧϰ����ǵ����ҡ����ҡ����к������������Ǻ���������ͼ1��ʾ��ֱ��������ABC����A����ǣ���ôsinA=![]() ��cosA=
��cosA=![]() ��tanA=
��tanA=![]() ��cotA=
��cotA=![]()
Ϊ���о���Ҫ�������ٴ���һ���Ƕ����涨һ���ǵ����Ǻ��������壺
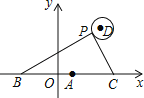
����һ�����������������Ķ�����Ϊԭ�㣬������ʼ����Ϊx���������ox������ֱ������ϵ��ͼ2�����ڽ������ձ�����ȡһ��P�����ĺ�������x����������y����P��ԭ�㣨0��0���ľ���Ϊr=![]() ��r�������ģ���Ȼ��ѽ��������Ǻ����涨Ϊ��sin��=
��r�������ģ���Ȼ��ѽ��������Ǻ����涨Ϊ��sin��=![]() ��cos��=
��cos��=![]() ��tan��=
��tan��=![]() ��cot��=
��cot��=![]()
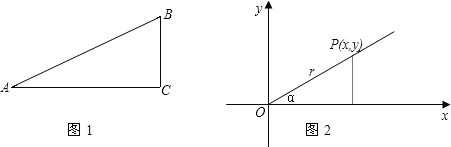
����֪����ͼ1���ĸ���ֵ�Ĵ�С���A�Ĵ�С�йأ�����ֱ�������εĴ�С�أ�ͬ��ͼ2���ĸ���ֵ�Ĵ�СҲ��������Ĵ�С�йأ������P�ڽ������ձ�λ���أ�
�Ƚ�ͼ1��ͼ2�����Կ���һ���ǵ����Ǻ�������������ֹ涨ʵ������һ���ģ����ݵڶ��ֶ���ش��������⣮
��1����90�㣼����180��������������Ǻ���ֵsin����cos����tan����cot��������ȡ��ֵ�����ļ�����
��2�����������ձ���ֱ��y=2x�غϣ���sin��+cos����ֵ��
��3���������Ƕ۽ǣ����ձ���һ��P��x��![]() ������cos��=
������cos��=![]() x����tan����ֵ��
x����tan����ֵ��
��4����0��ܦ���90������sin��+cos����ȡֵ��Χ��
���𰸡���1��sin������2��![]() ��
��![]() ����3��
����3��![]() ����4��1��sin��+cos����
����4��1��sin��+cos����![]() ��
��
��������
��1���ɵ�P��x��y���ڵڶ����ޣ��Ƴ�x��0��y��0������sin��=![]() ��cos��=
��cos��=![]() ��tan��=
��tan��=![]() ��cot��=
��cot��=![]() �������жϣ�
�������жϣ�
��2���������������ۼ��ɽ�����⣻
��3����ͼ2�У���PE��x����E����취���OE�ij����������Ǻ����Ķ��弴�ɽ�����⣻
��4������=0����90��ʱ���õ�sin��+cos������Сֵsin��+cos��=1������=45��ʱ���õ�sin��+cos�������ֵ��sin��+cos��=![]() ���ɴ˼��ɽ������.
���ɴ˼��ɽ������.
��1���ߵ�P��x��y���ڵڶ����ޣ�
��x��0��y��0��
��sin��=![]() ��cos��=
��cos��=![]() ��tan��=
��tan��=![]() ��cot��=
��cot��=![]() ��
��
��sin����0��cos����0��tan����0��cot����0��
��ȡȡ��ֵ����sin����
��2����ͼ1�У�
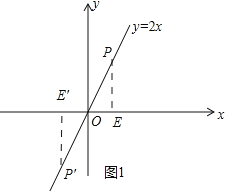
�ٵ���P�ڵ�һ����ʱ����PE��x����E����OE=a����PE=2a��OP=![]() a��
a��
��sin��+cos��=![]() ��
��
�ڵ���P�ڵ�������ʱ����PE��x����E����OE=a����PE=2a��OP=![]() a��
a��
��sin��+cos��=![]() ��
��
����������sin��+cos��=![]() ��
��![]() ��
��
��3����ͼ2�У���PE��x����E��
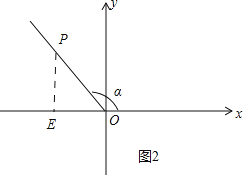
������PE=![]() ��cos��=
��cos��=![]() ��
��
��OP=2![]() ��
��
��OE=![]() ��
��
��tan��=![]() ��
��
��4������=0����90��ʱ���õ�sin��+cos������Сֵsin��+cos��=1��
����=45��ʱ���õ�sin��+cos�������ֵ��sin��+cos��=![]() ��
��
��1��sin��+cos����![]() ��
��