题目内容
 根据如图,利用面积法证明勾股定理.
根据如图,利用面积法证明勾股定理.考点:勾股定理的证明
专题:
分析:先利用“边角边”证明△ADE和△EBC全等,根据全等三角形对应角相等可得∠AED=∠CBE,再求出∠AEB=90°,然后根据梯形的面积公式和梯形的面积等于三个直角三角形的面积列出方程整理即可得证.
解答:证明:在△ADE和△EBC中,
,
∴△ADE≌△EBC(SAS),
∴∠AED=∠CBE,
∵∠CBE+∠BEC=90°,
∴∠AED+∠BEC=90°,
∴∠AEB=90°,
∴梯形的面积=
(a+b)(a+b)=2×
ab+
c2,
整理得a2+b2=c2.
|
∴△ADE≌△EBC(SAS),
∴∠AED=∠CBE,
∵∠CBE+∠BEC=90°,
∴∠AED+∠BEC=90°,
∴∠AEB=90°,
∴梯形的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
整理得a2+b2=c2.
点评:本题考查了勾股定理的证明,全等三角形的判定与性质,求出∠AEB=90°是解题的关键,难点在于利用梯形的面积列出方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
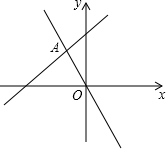 如图,函数y=-2x和y=kx+b的图象相交于点A(m,3),则关于x的不等式kx+b+2x>0的解集为( )
如图,函数y=-2x和y=kx+b的图象相交于点A(m,3),则关于x的不等式kx+b+2x>0的解集为( )A、x>
| ||
| B、x<m | ||
| C、x>m | ||
D、x>-
|