题目内容
13．
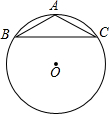如图，等腰三角形ABC内接于半径为5cm的⊙O，AB=AC，tanB=$\frac{1}{2}$，则AB为（ ）| A． | $\sqrt{10}$cm | B． | $\sqrt{5}$cm | C． | 2$\sqrt{10}$cm | D． | 2$\sqrt{5}$cm |
分析 连接OA交BC于D，连接OB，根据tanB=$\frac{1}{2}$，得到BD=2AD，设AD=x，表示出BD，在Rt△OBD中，运用勾股定理列出关于x的方程，解方程求出x的值，求出AB即可．
解答 
解：连接OA交BC于D，连接OB，
∵AB=AC，
∴OA⊥BC，
∵tanB=$\frac{1}{2}$，
∴BD=2AD，
设AD=x，则BD=2x，AB=$\sqrt{5}$x，OD=5-x，
在Rt△OBD中，
OB2=OD2+BD2，
即25=（5-x）2+4x2，
解得，x=2，
∴AB=2$\sqrt{5}$，
故选：D．
点评 本题考查的是垂径定理和勾股定理的运用，正确作出辅助线构造直角三角形运用垂径定理和勾股定理是解题的关键．
练习册系列答案
优化作业上海科技文献出版社系列答案
相关题目
3．要判断马力同学的数学考试成绩是否稳定，那么需要知道他最近连续几次数学考试成绩的（ ）
| A． | 方差 | B． | 中位数 | C． | 平均数 | D． | 众数 |
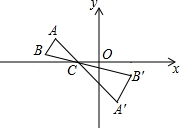如图，△ABC中，A，B两个顶点在x轴的上方，点C的坐标是（-1，0），以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B′C，并把△ABC的边长放大到原来的2倍．设点B的对应点B′的横坐标是2，则点B的横坐标是-2.5．
1．若一个反比例函数的图象与一次函数y=x-3的图象在同一平面直角坐标系中没有公共点，则这个反比例函数的解析式可能是（ ）
| A． | y=$\frac{3}{x}$ | B． | y=-$\frac{3}{x}$ | C． | y=$\frac{1}{x}$ | D． | y=-$\frac{1}{x}$ |
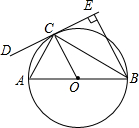如图，AB是⊙O的直径，CD是⊙O的切线，切点为C，BE⊥CD，垂足为E，连接AC、BC．
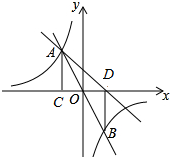如图，在直角坐标系xOy中，直线y=mx与双曲线y=$\frac{n}{x}$相交于A（-1，a）、B两点，AC⊥x轴，垂足为C，BD⊥x轴，垂足为D，且满足tan∠AOC=2．
5．下列运算正确的是（ ）
| A． | （x-2）2=x2-4 | B． | x3•x4=x12 | C． | x6÷x3=x2 | D． | （x2）3=x6 |
