题目内容
1.若一个反比例函数的图象与一次函数y=x-3的图象在同一平面直角坐标系中没有公共点,则这个反比例函数的解析式可能是( )| A. | y=$\frac{3}{x}$ | B. | y=-$\frac{3}{x}$ | C. | y=$\frac{1}{x}$ | D. | y=-$\frac{1}{x}$ |
分析 设反比例函数解析式为y=$\frac{k}{x}$,根据反比例函数与一次函数的交点问题,方程组$\left\{\begin{array}{l}{y=\frac{k}{x}}\\{y=x-3}\end{array}\right.$没有实数解,消去y整理得到x2-3x-k=0,根据判别式的意义得到△=(-3)2-4(-k)<0,解得k<-$\frac{9}{4}$,然后对四个选项进行判断.
解答 解:设反比例函数解析式为y=$\frac{k}{x}$,
根据题意方程组$\left\{\begin{array}{l}{y=\frac{k}{x}}\\{y=x-3}\end{array}\right.$没有实数解,
则方程x-3=$\frac{k}{x}$无解,
方程变形为x2-3x-k=0,
所以△=(-3)2-4(-k)<0,解得k<-$\frac{9}{4}$.
故选B.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
11.下列结论不正确的是( )
| A. | $\overrightarrow{AB}$+$\overrightarrow{BA}$=0 | B. | $\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{b}$+$\overrightarrow{a}$ | ||
| C. | 如果$\overrightarrow{AB}$=$\overrightarrow{CD}$,那么|$\overrightarrow{AB}$|=|$\overrightarrow{CD}$| | D. | 如果非零向量$\overrightarrow{a}$=k$\overrightarrow{b}$(k≠0),那么$\overrightarrow{a}$∥$\overrightarrow{b}$ |
9.为了解峨边今年参加中考的1000名学生的体重情况,抽查了其中200名学生的体重进行统计分析,下列叙述正确的是( )
| A. | 200名学生是总体 | |
| B. | 200名学生的体重是总体的一个样本 | |
| C. | 每名学生是总体的一个个体 | |
| D. | 以上调查是普查 |
13.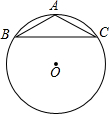 如图,等腰三角形ABC内接于半径为5cm的⊙O,AB=AC,tanB=$\frac{1}{2}$,则AB为( )
如图,等腰三角形ABC内接于半径为5cm的⊙O,AB=AC,tanB=$\frac{1}{2}$,则AB为( )
 如图,等腰三角形ABC内接于半径为5cm的⊙O,AB=AC,tanB=$\frac{1}{2}$,则AB为( )
如图,等腰三角形ABC内接于半径为5cm的⊙O,AB=AC,tanB=$\frac{1}{2}$,则AB为( )| A. | $\sqrt{10}$cm | B. | $\sqrt{5}$cm | C. | 2$\sqrt{10}$cm | D. | 2$\sqrt{5}$cm |
10.2014年中国吸引外国投资达1280亿美元,成为全球外国投资第一大目的地国,将1280亿美元用科学记数法表示为( )
| A. | 12.8×1010美元 | B. | 1.28×1011美元 | C. | 1.28×1012美元 | D. | 0.128×1013美元 |
11.某市户籍人口1694000人,则该市户籍人口数据用科学记数法可表示为( )
| A. | 1.694×104人 | B. | 1.694×105人 | C. | 1.694×106人 | D. | 1.694×107人 |
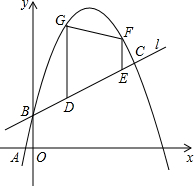 如图,已知一次函数y1=$\frac{1}{2}$x+b的图象l与二次函数y2=-x2+mx+b的图象l′都经过点B(0,1)和点C,且图象l′过点A(2-$\sqrt{5}$,0).
如图,已知一次函数y1=$\frac{1}{2}$x+b的图象l与二次函数y2=-x2+mx+b的图象l′都经过点B(0,1)和点C,且图象l′过点A(2-$\sqrt{5}$,0).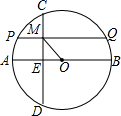 已知AB是⊙O的直径,弦CD⊥AB于点E,弦PQ∥AB交弦CD于点M,BE=18,CD=PQ=24,则OM的长为5$\sqrt{2}$.
已知AB是⊙O的直径,弦CD⊥AB于点E,弦PQ∥AB交弦CD于点M,BE=18,CD=PQ=24,则OM的长为5$\sqrt{2}$.