题目内容
8.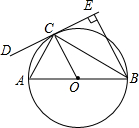 如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,连接AC、BC.
如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,连接AC、BC.(1)求证:BC平分∠ABE;
(2)若∠ABC=30°,OA=4,求CE的长.
分析 (1)利用切线的性质首先得出∠OCB=∠CBE,进而得出∠CBE=∠OBC即可求出BC平分∠ABE;
(2)过A做CF⊥AB于F由AB是⊙O的直径得到∠ACB=90°由于∠ABC=30°得到∠A=60°于是得到AC=$\frac{1}{2}$AB=OA=4在Rt△ACF中,∠A=60°,根据$\frac{CF}{AC}=sin60°=\frac{\sqrt{3}}{2}$,求出CF=AC•$\frac{\sqrt{3}}{2}$=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,再由角平分线的性质即可得到结果.
解答 证明:(1)∵CD是⊙O切线,
∴OC⊥CD,
∴∠OCB+∠BCE=90°,
∵BE⊥CD,
∴∠CBE+∠BCE=90°,
∴∠OCB=∠CBE,
又∵OC=OB,
∴∠OCB=∠OBC,
∴∠CBE=∠OBC,
即BC平分∠ABE;
(2)过A做CF⊥AB于F,
∵AB是⊙O的直径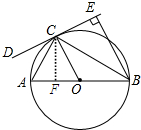 ,
,
∴∠ACB=90°,
∵∠ABC=30°,
∴∠A=60°
∴AC=$\frac{1}{2}$AB=OA=4,
在Rt△ACF中,∠A=60°,
∴$\frac{CF}{AC}=sin60°=\frac{\sqrt{3}}{2}$,
∴CF=AC•$\frac{\sqrt{3}}{2}$=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∵BC平分∠ABE,CF⊥AB,
∵CE⊥BE,
∴CE=CF=2$\sqrt{3}$.
点评 此题主要考查了切线的性质以及锐角三角函数,根据切线的性质得出∠OCB=∠CBE是解题关键.

练习册系列答案
相关题目
18.对于反比例函数y=-$\frac{1}{x}$,下列说法不正确的是( )
| A. | 图象经过点(1,-1) | B. | 图象在第二、四象限 | ||
| C. | x>0时,y随x的增大而增大 | D. | x<0时,y随x的增大而减小 |
19.若$\sqrt{3x-6}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥-2 | B. | x≠-2 | C. | x≥2 | D. | x≠2 |
13.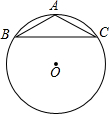 如图,等腰三角形ABC内接于半径为5cm的⊙O,AB=AC,tanB=$\frac{1}{2}$,则AB为( )
如图,等腰三角形ABC内接于半径为5cm的⊙O,AB=AC,tanB=$\frac{1}{2}$,则AB为( )
 如图,等腰三角形ABC内接于半径为5cm的⊙O,AB=AC,tanB=$\frac{1}{2}$,则AB为( )
如图,等腰三角形ABC内接于半径为5cm的⊙O,AB=AC,tanB=$\frac{1}{2}$,则AB为( )| A. | $\sqrt{10}$cm | B. | $\sqrt{5}$cm | C. | 2$\sqrt{10}$cm | D. | 2$\sqrt{5}$cm |
17.已知下列命题:
①在Rt△ABC中,∠C=90°,若∠A>∠B,则sinA>sinB;
②四条线段a,b,c,d中,若$\frac{a}{b}$=$\frac{c}{d}$,则ad=bc;
③若a>b,则a(m2+1)>b(m2+1);
④若|-x|=-x,则x≥0.
其中原命题与逆命题均为真命题的是( )
①在Rt△ABC中,∠C=90°,若∠A>∠B,则sinA>sinB;
②四条线段a,b,c,d中,若$\frac{a}{b}$=$\frac{c}{d}$,则ad=bc;
③若a>b,则a(m2+1)>b(m2+1);
④若|-x|=-x,则x≥0.
其中原命题与逆命题均为真命题的是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
18.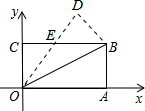 如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合,OD与BC交于点E,则点D的坐标是( )
如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合,OD与BC交于点E,则点D的坐标是( )
 如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合,OD与BC交于点E,则点D的坐标是( )
如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合,OD与BC交于点E,则点D的坐标是( )| A. | (4,8) | B. | (5,8) | C. | ($\frac{24}{5}$,$\frac{32}{5}$) | D. | ($\frac{22}{5}$,$\frac{36}{5}$) |
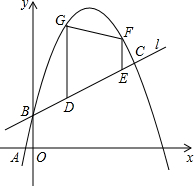 如图,已知一次函数y1=$\frac{1}{2}$x+b的图象l与二次函数y2=-x2+mx+b的图象l′都经过点B(0,1)和点C,且图象l′过点A(2-$\sqrt{5}$,0).
如图,已知一次函数y1=$\frac{1}{2}$x+b的图象l与二次函数y2=-x2+mx+b的图象l′都经过点B(0,1)和点C,且图象l′过点A(2-$\sqrt{5}$,0).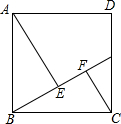 如图,正方形ABCD的边长是10,点G是CD边上任意一点,AE⊥BG于点E,CF⊥BG于点F,AE=8.
如图,正方形ABCD的边长是10,点G是CD边上任意一点,AE⊥BG于点E,CF⊥BG于点F,AE=8.