Question

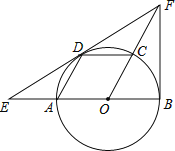
【题目】如图，在Rt△ABC中，∠C=90°，AD是∠BAC的角平分线．

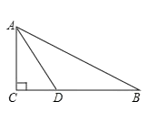
(1) 用无刻度的直尺和圆规过A、D两点作⊙O，使圆心O在AB边上 (保留画图痕迹，不写画法)

(2) 求证：BC为⊙O的切线；

(3) 如果AC=3，tanB=，求⊙O的半径．

Answer 1

【答案】（1）图见解析（2）见解析（3）

【解析】

(1)因为AD是弦，所以圆心O即在AB上，也在AD的垂直平分线上；

(2)因为D在圆上，所以只要能证明OD⊥BC就说明BC为⊙O的切线；

(3)根据∠B的正切值，先求出BC、AB的值，再结合三角形相似就可求出圆的半径的长．

解答

(1)如图所示，

(2)连接OD，

∵AD平分∠CAB，

∴∠CAD=∠BAD，

又∵OA=OD，

∴∠OAD=∠ODA，

∴∠CAD=∠ODA，

∴OD//AC，

∴∠ODB=∠C=90，

又∵OD为半径，

∴BC是⊙O的切线.

(3)∵AC=3，tanB=

∴BC=4，

∴AB=5，

设⊙O的半径为r，则OA=OD=r，BO=5r，

∵OD//AC，

∴△BOD∽△BAC，

∴

即，

解得，r=，

∴⊙O的半径为．