题目内容
【题目】已知顶点为![]() 的抛物线
的抛物线![]() 经过点
经过点![]() .
.
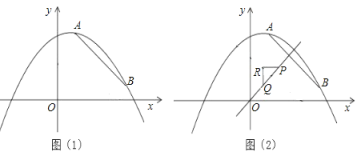
(1)求抛物线的解析式;
(2)设![]() ,
,![]() 分别是
分别是![]() 轴、
轴、![]() 轴上的两个动点.
轴上的两个动点.
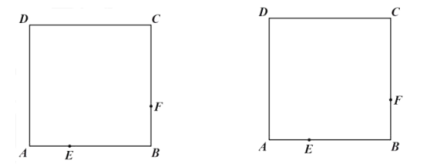
①当四边形![]() 的周长最小时,在图1中作直线
的周长最小时,在图1中作直线![]() ,保留作图痕迹.并直接写出直线
,保留作图痕迹.并直接写出直线![]() 的解析式;
的解析式;
②点![]() 是直线
是直线![]() 上的一个动点,
上的一个动点,![]() 是
是![]() 的中点,以
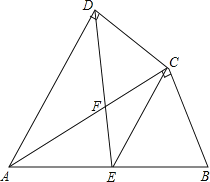
的中点,以![]() 为斜边按图2所示构造等腰
为斜边按图2所示构造等腰![]() .在①的条件下,记
.在①的条件下,记![]() 与
与![]() 的公共部分的面积为
的公共部分的面积为![]() .求
.求![]() 关于
关于![]() 的函数关系式,并求
的函数关系式,并求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)①作图见解析;
;(2)①作图见解析;![]() ;②S
;②S![]() ;
;![]() 的最大值为
的最大值为![]() .
.
【解析】
(1)设出顶点式,直接将B点代入即可完成解答;
(2)①过y,x轴分别做A,B的对称点![]() 、
、![]() ,然后连
,然后连![]() 、
、![]() ,当这四点在同一直线时,周长最小,即可画出图形;再确定
,当这四点在同一直线时,周长最小,即可画出图形;再确定![]() 、
、![]() ,由待定系数法即可得到直线
,由待定系数法即可得到直线![]() 、
、![]() 的解析式,即为直线CD的解析式;
的解析式,即为直线CD的解析式;
②由①得到直线CD的解析式,即可求出CD与直线y=x的交点坐标,得到△PQR与直线y=x有公共点时x的取值范围,以及公共部分的面积s与x之间的函数关系式,然后根据二次函数确定其最大值即可。
(1)根据题意,设物线的顶点式为![]() ,
,
将![]() 代入得,
代入得,![]() ,
,
∴抛物线解析式为:![]() .
.
(2)①作图如下:
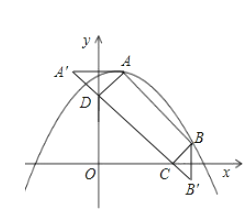
直线![]() 的解析式为
的解析式为![]() .
.
②如下图:
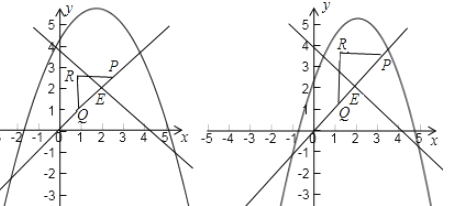
点![]() ,当
,当![]() 时,
时,![]() ,
,
解得![]() ,
,
当![]() 时,
时,![]()
![]()
![]() .
.
∴当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
![]() ,
,
即![]() 时,
时,![]() ,
,
综上:![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目