题目内容
6．
如图，在△ABC中，∠C=90°，AC=BC，点D在AC上，且∠DBC=30°，求$\frac{AD}{AB}$的值．
分析 由三角函数的定义知BC=$\sqrt{3}$CD，则BC=（$\sqrt{3}$-1）CD，由AC=BC，可求得结论．
解答 解：设CD=x，
∵∠C=90°，∠DBC=30°，
∴BC=$\sqrt{3}$x，
∵AC=BC，
∴AC=$\sqrt{3}$x，
AB=$\sqrt{2}$AC=$\sqrt{6}$x
∴AD=（$\sqrt{3}$-1）x，
∴$\frac{AD}{AB}$=$\frac{（\sqrt{3}-1）x}{\sqrt{6}x}$=$\frac{3\sqrt{2}-\sqrt{6}}{6}$．
点评 本题主要考查了三角函数的定义，等腰直角三角形的性质，灵活掌握三角函数的定义是解决问题的关键．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
17．下列根式是最简二次根式的是（ ）
| A． | $\sqrt{0.3}$ | B． | $\sqrt{{a}^{2}-{b}^{2}}$ | C． | $\sqrt{{a}^{2}b}$ | D． | $\sqrt{12}$ |
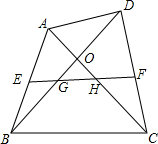如图，在四边形ABCD中，AC与BD交于点O，E为AB中点，F为CD中点，EF分别与BD、AC交于点G、H．
如图，E是四边形ADBC内的一点，连接AE，CE，DE，AB，如果$\frac{DE}{BC}$=$\frac{AE}{AC}$=$\frac{AD}{AB}$，△ADB与△AEC相似吗？为什么？
15．在下列多项式乘法中，不能用平方差公式计算的是（ ）
| A． | （a-b）（-a+b） | B． | （m3-n3）（m3+n3） | C． | （-7-x）（7-x） | D． | （x2-y2）（y2+x2） |