题目内容
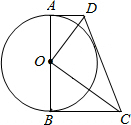 如图,已知直角梯形ABCD,∠B=90°,AD∥BC,以AB为直径作⊙O,连接OD,并且OD平分∠ADO.
如图,已知直角梯形ABCD,∠B=90°,AD∥BC,以AB为直径作⊙O,连接OD,并且OD平分∠ADO.(1)求证:⊙O与CD相切.
(2)若OC=12,OD=5,求⊙O的半径.
考点:切线的判定
专题:
分析:(1)过O作OE垂直于CD,根据梯形的面积公式表示出梯形ABCD的面积,由O为AB的中点,将AB换为2OA,变形得到梯形的面积等于△OAD与△OBC的面积之和的2倍,又梯形ABCD的面积=△AOD的面积+△BOC的面积+△COD的面积,得到△COD的面积=△AOD的面积+△BOC的面积,而△AOD与△BOC都为直角三角形,△COD的面积等于CD乘以OE除以2,分别利用三角形的面积公式表示后,根据AD+BC=CD,得到OA=OE,又OA为圆O的半径,故得到CD过半径OE的端点E,且与半径OE垂直,进而确定出CD为圆O的切线;
(2)取CD的中点F,连接OF,又O为AB的中点,得到OF为梯形的中位线,利用梯形中位线定理得到OF等于上下底之和的一半,再利用AD+BC=CD变形,得到OF为CD的一半,即OF等于以CD为直径的圆F的半径,根据直径所对的圆周角为直角得到∠DOC为直角,在直角三角形COD中,由OD与OC的长,利用勾股定理即可求出CD的长即可.
(2)取CD的中点F,连接OF,又O为AB的中点,得到OF为梯形的中位线,利用梯形中位线定理得到OF等于上下底之和的一半,再利用AD+BC=CD变形,得到OF为CD的一半,即OF等于以CD为直径的圆F的半径,根据直径所对的圆周角为直角得到∠DOC为直角,在直角三角形COD中,由OD与OC的长,利用勾股定理即可求出CD的长即可.
解答:(1)证明:过AB的中点O作OE⊥CD于E,

∵S梯形ABCD=
(AD+BC)•AB=(AD+BC)•OA=2(
AD•OA+
BC•OB)=2(S△OAD+S△OBC),
且S梯形ABCD=S△OBC+S△OAD+S△OCD,
∴S△OBC+S△OAD=S△OCD,且OA=OB,
∴
AD•OA+
BC•OB=
AD•OA+
BC•OA=
(AD+BC)•OA=
CD•OE,
又∵AD+BC=CD,
∴OA=OE,
∴E点在以AB为直径的⊙O上,
又∵OE⊥CD,
∴CD是⊙O的切线,即CD与⊙O相切;
(2)解:在CD上取中点F,连接OF,
过D作DM⊥BC于M,
则AB=DM,AD=BM,∠DMC=90°
∵OF为梯形ABCD的中位线,且AD+BC=CD,
∴OF=
(AD+BC)=
CD,
∴O点在以CD为直径的⊙F上,
∴∠COD=90°,
在Rt△COD中,OD=6cm,OC=8cm,
∴根据勾股定理得:CD=
=
=13,
OF=6.5,
设⊙O半径为R,
则
AD×OA+
DO×OC+
OB×BC=
×(AD+BC)×2R
所以
R×13+
×5×12=
×13×2R,
解得:R=
,
即⊙O的半径为
.

∵S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
且S梯形ABCD=S△OBC+S△OAD+S△OCD,
∴S△OBC+S△OAD=S△OCD,且OA=OB,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵AD+BC=CD,
∴OA=OE,
∴E点在以AB为直径的⊙O上,
又∵OE⊥CD,
∴CD是⊙O的切线,即CD与⊙O相切;
(2)解:在CD上取中点F,连接OF,

过D作DM⊥BC于M,
则AB=DM,AD=BM,∠DMC=90°
∵OF为梯形ABCD的中位线,且AD+BC=CD,
∴OF=
| 1 |
| 2 |
| 1 |
| 2 |
∴O点在以CD为直径的⊙F上,
∴∠COD=90°,
在Rt△COD中,OD=6cm,OC=8cm,
∴根据勾股定理得:CD=
| OD2+OC2 |
| 52+122 |
OF=6.5,
设⊙O半径为R,
则
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:R=
| 60 |
| 13 |
即⊙O的半径为
| 60 |
| 13 |
点评:此题考查了切线的性质与判定,勾股定理,梯形的中位线定理,以及梯形、三角形面积的计算,其中作出相应的辅助线是解本题的关键.

练习册系列答案
相关题目
 如图所示,在正方形ABCD中,若对角线长为10cm,则PE+PF=
如图所示,在正方形ABCD中,若对角线长为10cm,则PE+PF=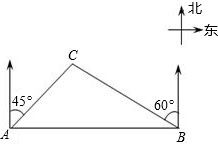 某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图所示,在A地北偏东45°、B地北偏西60°方向上有一牧民区C.求牧民区C到B地的距离.
某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图所示,在A地北偏东45°、B地北偏西60°方向上有一牧民区C.求牧民区C到B地的距离. “玉兔号”月球车成功实现月球探月,是全中国人民的骄傲!航天米小刚同学为了庆祝中国玉兔号成功探月,精心制作了一个正方体盒子,并在该正方体盒子的每个面上都写有一个字,分别是:中、国、造、玉、兔、车,其平面展开图如图所示,那么在该正方体盒子中,和“中”字相对的面所写的字是
“玉兔号”月球车成功实现月球探月,是全中国人民的骄傲!航天米小刚同学为了庆祝中国玉兔号成功探月,精心制作了一个正方体盒子,并在该正方体盒子的每个面上都写有一个字,分别是:中、国、造、玉、兔、车,其平面展开图如图所示,那么在该正方体盒子中,和“中”字相对的面所写的字是