题目内容
在△ABC中,AB=5cm,AC=4cm,AB和AC的夹角为α,设△ABC的面积为S,
(1)若α为锐角,求S关于α的函数表达式;若α为钝角呢?
(2)何时△ABC的面积最大,最大面积为多少?
(1)若α为锐角,求S关于α的函数表达式;若α为钝角呢?
(2)何时△ABC的面积最大,最大面积为多少?
考点:解直角三角形
专题:
分析:(1)分别作CD⊥AB,根据α的值可以求得CD的长,即可计算S的值;
(2)根据sinα有最大值1即可求得S的最大值,即可解题.
(2)根据sinα有最大值1即可求得S的最大值,即可解题.
解答:解: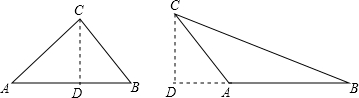
(1)①若α为锐角,作CD⊥AB,则CD=AC•sinA=4sinα,
∴S=
AB•CD=
×5×4sinα=10sinα;
②若α为钝角呢,作CD⊥AB,则CD=AC•sinA=4sin(180°-α)=4sinα,
∴S=
AB•CD=
×5×4sinα=10sinα;
(2)∵S=10sinα,
∴sinα有最大值时S有最大值,
∵sinα最大值为1,
∴S有最大值为10.

(1)①若α为锐角,作CD⊥AB,则CD=AC•sinA=4sinα,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
②若α为钝角呢,作CD⊥AB,则CD=AC•sinA=4sin(180°-α)=4sinα,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵S=10sinα,
∴sinα有最大值时S有最大值,
∵sinα最大值为1,
∴S有最大值为10.
点评:本题考查了三角形中正弦函数的运用,考查了三角形面积的计算,考查了正弦值的最值问题,本题中求得CD的长是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
已知点A(2,-3)关于y轴对称的点的坐标为点B,则点B的坐标( )
| A、(2,-3) |
| B、(-2,-3) |
| C、(2,3) |
| D、(-2,3) |
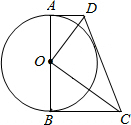 如图,已知直角梯形ABCD,∠B=90°,AD∥BC,以AB为直径作⊙O,连接OD,并且OD平分∠ADO.
如图,已知直角梯形ABCD,∠B=90°,AD∥BC,以AB为直径作⊙O,连接OD,并且OD平分∠ADO. 如图,△ABC中,AC=AB,以AB为直径作⊙O,交BC于D,交AC于E,试说明∠BAD和∠EDC之间的数量关系.
如图,△ABC中,AC=AB,以AB为直径作⊙O,交BC于D,交AC于E,试说明∠BAD和∠EDC之间的数量关系.