题目内容
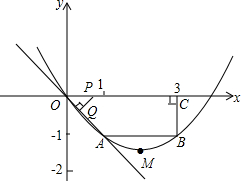 已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,-1),B(3,-1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动.过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.
已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,-1),B(3,-1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动.过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.(1)求经过O、A、B三点的抛物线的解析式,并确定顶点M的坐标;
(2)用含t的代数式表示点P、点Q的坐标;
(3)如果将△OPQ绕着点P按逆时针方向旋转90°,是否存在t,使得△OPQ的顶点O或顶点Q在抛物线上?若存在,请求出t的值;若不存在,请说明理由;
(4)求出S与t的函数关系式.
考点:二次函数综合题,三角形的面积,等腰直角三角形
专题:压轴题
分析:(1)设抛物线解析式为y=ax2+bx(a≠0),然后把点A、B的坐标代入求出a、b的值,即可得解,再把函数解析式整理成顶点式形式,然后写出顶点M的坐标;
(2)根据点P的速度求出OP,即可得到点P的坐标,再根据点A的坐标求出∠AOC=45°,然后判断出△POQ是等腰直角三角形,根据等腰直角三角形的性质求出点Q的坐标即可;
(3)根据旋转的性质求出点O、Q的坐标,然后分别代入抛物线解析式,求解即可;
(4)求出点Q与点A重合时的t=1,点P与点C重合时的t=1.5,t=2时PQ经过点B,然后分①0<t≤1时,重叠部分的面积等于△POQ的面积,②1<t≤1.5时,重叠部分的面积等于两个等腰直角三角形的面积的差,③1.5<t<2时,重叠部分的面积等于梯形的面积减去一个等腰直角三角形的面积分别列式整理即可得解.
(2)根据点P的速度求出OP,即可得到点P的坐标,再根据点A的坐标求出∠AOC=45°,然后判断出△POQ是等腰直角三角形,根据等腰直角三角形的性质求出点Q的坐标即可;
(3)根据旋转的性质求出点O、Q的坐标,然后分别代入抛物线解析式,求解即可;
(4)求出点Q与点A重合时的t=1,点P与点C重合时的t=1.5,t=2时PQ经过点B,然后分①0<t≤1时,重叠部分的面积等于△POQ的面积,②1<t≤1.5时,重叠部分的面积等于两个等腰直角三角形的面积的差,③1.5<t<2时,重叠部分的面积等于梯形的面积减去一个等腰直角三角形的面积分别列式整理即可得解.
解答:解:(1)设抛物线解析式为y=ax2+bx(a≠0),
把点A(1,-1),B(3,-1)代入得,
,
解得
,
∴抛物线解析式为y=
x2-
x,
∵y=
x2-
x=
(x-2)2-
,
∴顶点M的坐标为(2,-
);
(2)∵点P从点O出发速度是每秒2个单位长度,
∴OP=2t,
∴点P的坐标为(2t,0),
∵A(1,-1),
∴∠AOC=45°,
∴点Q到x轴、y轴的距离都是
OP=
×2t=t,
∴点Q的坐标为(t,-t);

(3)∵△OPQ绕着点P按逆时针方向旋转90°,
∴旋转后点O、Q的对应点的坐标分别为(2t,-2t),(3t,-t),
若顶点O在抛物线上,则
×(2t)2-
×(2t)=-2t,
解得t=
(t=0舍去),
∴t=
时,点O(1,-1)在抛物线y=
x2-
x上,
若顶点Q在抛物线上,则
×(3t)2-
×(3t)=-t,
解得t=1(t=0舍去),
∴t=1时,点Q(3,-1)在抛物线y=
x2-
x上.
(4)点Q与点A重合时,OP=1×2=2,t=2÷2=1,
点P与点C重合时,OP=3,t=3÷2=1.5,
t=2时,OP=2×2=4,PC=4-3=1,此时PQ经过点B,
所以,分三种情况讨论:
①0<t≤1时,S=S△OPQ=
×(2t)×
=t2,
②1<t≤1.5时,S=S△OP′Q′-S△AEQ′=
×(2t)×
-
×(
t-
)2=2t-1;
③1.5<t<2时,S=S梯形OABC-S△BGF=
×(2+3)×1-
×[1-(2t-3)]2=-2(t-2)2+
=-2t2+8t-
;
所以,S与t的关系式为S=
.
把点A(1,-1),B(3,-1)代入得,
|
解得
|
∴抛物线解析式为y=
| 1 |
| 3 |
| 4 |
| 3 |
∵y=
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
∴顶点M的坐标为(2,-
| 4 |
| 3 |
(2)∵点P从点O出发速度是每秒2个单位长度,
∴OP=2t,
∴点P的坐标为(2t,0),
∵A(1,-1),
∴∠AOC=45°,
∴点Q到x轴、y轴的距离都是
| 1 |
| 2 |
| 1 |
| 2 |
∴点Q的坐标为(t,-t);

(3)∵△OPQ绕着点P按逆时针方向旋转90°,
∴旋转后点O、Q的对应点的坐标分别为(2t,-2t),(3t,-t),
若顶点O在抛物线上,则
| 1 |
| 3 |
| 4 |
| 3 |
解得t=
| 1 |
| 2 |
∴t=
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 3 |
若顶点Q在抛物线上,则
| 1 |
| 3 |
| 4 |
| 3 |
解得t=1(t=0舍去),
∴t=1时,点Q(3,-1)在抛物线y=
| 1 |
| 3 |
| 4 |
| 3 |
(4)点Q与点A重合时,OP=1×2=2,t=2÷2=1,

点P与点C重合时,OP=3,t=3÷2=1.5,
t=2时,OP=2×2=4,PC=4-3=1,此时PQ经过点B,
所以,分三种情况讨论:
①0<t≤1时,S=S△OPQ=
| 1 |
| 2 |
| 2t |
| 2 |
②1<t≤1.5时,S=S△OP′Q′-S△AEQ′=
| 1 |
| 2 |
| 2t |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
③1.5<t<2时,S=S梯形OABC-S△BGF=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 11 |
| 2 |
所以,S与t的关系式为S=
|
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,等腰直角三角形的性质,二次函数图象上点的坐标特征,三角形的面积,难点在于(4)随着运动时间的变化,根据重叠部分的形状的不同分情况讨论,作出图形更形象直观.

练习册系列答案
相关题目
在下列图案中,不是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).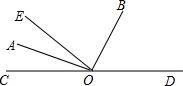 如图,O是直线CD上一点,OA平分∠EOC,OB平分∠EOD.
如图,O是直线CD上一点,OA平分∠EOC,OB平分∠EOD.