题目内容
5.甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图: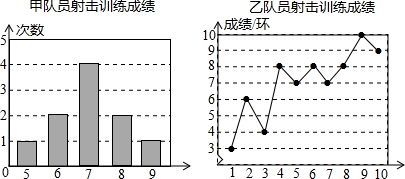
根据以上信息,整理分析数据如下:
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | 7 | 7 | 7 | 1.2 |
| 乙 | 7 | 7.5 | 8 | 4.2 |
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
分析 (1)利用平均数的计算公式直接计算平均分即可;将乙的成绩从小到大重新排列,用中位数的定义直接写出中位数即可;根据乙的平均数利用方差的公式计算即可;
(2)结合平均数和中位数、众数、方差三方面的特点进行分析.
解答 解:(1)甲的平均成绩a=$\frac{5×1+6×2+7×4+8×2+9×1}{1+2+4+2+1}$=7(环),
∵乙射击的成绩从小到大重新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数b=$\frac{7+8}{2}$=7.5(环),
其方差c=$\frac{1}{10}$×[(3-7)2+(4-7)2+(6-7)2+2×(7-7)2+3×(8-7)2+(9-7)2+(10-7)2]
=$\frac{1}{10}$×(16+9+1+3+4+9)
=4.2,
完成表格如下:
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | 7 | 7 | 7 | 1.2 |
| 乙 | 7 | 7.5 | 8 | 4.2 |
综合以上各因素,若选派一名队员参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
点评 本题考查的是条形统计图和方差、平均数、中位数、众数的综合运用.熟练掌握平均数的计算,理解方差的概念,能够根据计算的数据进行综合分析.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
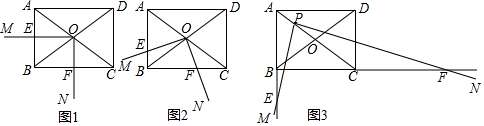
20. 如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF,以下结论不正确的是( )
如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF,以下结论不正确的是( )
 如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF,以下结论不正确的是( )
如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF,以下结论不正确的是( )| A. | AD∥BC | B. | ∠ACB=2∠ADB | C. | ∠ADC=90°-∠ABD | D. | BD平分∠ADC |
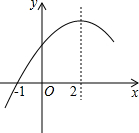 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)若点A(-3,y1)、点B(-$\frac{1}{2}$,y2)、点C($\frac{7}{2}$,y3)在该函数图象上,则y1<y3<y2;(4)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确结论的序号是①④.
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)若点A(-3,y1)、点B(-$\frac{1}{2}$,y2)、点C($\frac{7}{2}$,y3)在该函数图象上,则y1<y3<y2;(4)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确结论的序号是①④.