题目内容
某商品的进价为每件40元,售价每件不低于60元且每件不高于80元.当售价为每件60元是,每个月可卖出100件;如果每件商品的售价每上涨1元,则每个月少卖2件.设每件商品的售价为x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)当每件商品定价为多少元使得每个月的利润恰为2250元?
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)当每件商品定价为多少元使得每个月的利润恰为2250元?
考点:二次函数的应用
专题:
分析:(1)由于售价为60时,每个月卖100件,售价上涨影响销量,因此根据60≤x≤80列式求解;
(2)由(1)中求得的函数解析式来根据自变量x的范围求利润的最大值;
(3)在60≤x≤80,令y=2250,求得定价x的值.
(2)由(1)中求得的函数解析式来根据自变量x的范围求利润的最大值;
(3)在60≤x≤80,令y=2250,求得定价x的值.
解答:解:(1)y=(x-40)[100+2(60-x)]=-2x2+300x-8800;(60≤x≤80且x为整数)
(2)y=-2x2+300x-8800=-2(x-75)2+2450,
∵a=-2<0,
∴当x=75时,y有最大值2450.
∴每件商品的售价定为75元时,每个月可获得最大利润,最大的月利润是2450元.
(3)当y=2250元时,
-2x2+300x-8800=2250,
解得:x1=65,x2=85;
其中,x2=85不符合题意,舍去.
因此当每件商品的售价为65元时,每个月的利润恰为2250元.
(2)y=-2x2+300x-8800=-2(x-75)2+2450,
∵a=-2<0,
∴当x=75时,y有最大值2450.
∴每件商品的售价定为75元时,每个月可获得最大利润,最大的月利润是2450元.
(3)当y=2250元时,
-2x2+300x-8800=2250,
解得:x1=65,x2=85;
其中,x2=85不符合题意,舍去.
因此当每件商品的售价为65元时,每个月的利润恰为2250元.
点评:此题考查二次函数的实际运用,利用基本数量关系求出函数解析式是解决问题的关键.

练习册系列答案
相关题目
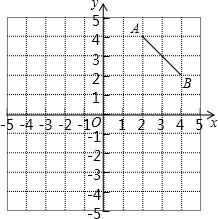 如图在8×8的正方形网格中建立直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.
如图在8×8的正方形网格中建立直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形. 如图,抛物线y=-x2+2(m+1)x+m+3与x轴交于A,B两点,且OA:OB=1:3,求m的值.
如图,抛物线y=-x2+2(m+1)x+m+3与x轴交于A,B两点,且OA:OB=1:3,求m的值. 如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O,若△COD的面积为a2,△AOB的面积为b2,其中a>0,b>0.求△AOD的面积.
如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O,若△COD的面积为a2,△AOB的面积为b2,其中a>0,b>0.求△AOD的面积.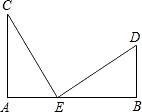 已知,如图,AC⊥AB,DB⊥AB,AC=BE,AE=BD,
已知,如图,AC⊥AB,DB⊥AB,AC=BE,AE=BD,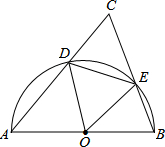 如图,在△ABC中,∠C=60°,以AB为直径的半圆O分别交AC、BC于点D、E.
如图,在△ABC中,∠C=60°,以AB为直径的半圆O分别交AC、BC于点D、E. 已知:如图,点P是△ABC的重心,过P作AC的平行线,分别交AB,BC于点D,E,作DF∥EC,交AC于点F,若△ABC的面积为18cm2,求四边形ECFD的面积.
已知:如图,点P是△ABC的重心,过P作AC的平行线,分别交AB,BC于点D,E,作DF∥EC,交AC于点F,若△ABC的面积为18cm2,求四边形ECFD的面积.