题目内容
5.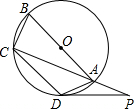 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.(Ⅰ)若AB=4,求$\widehat{CD}$的长;
(Ⅱ)若$\widehat{BC}$=$\widehat{AD}$,AD=AP,求证:PD是⊙O的切线.
分析 (Ⅰ)连接OC,OD,由圆周角定理得到∠COD=2∠CAD,∠CAD=45°,于是得到∠COD=90°,根据弧长公式即可得到结论;
(Ⅱ)由已知条件得到∠BOC=∠AOD,由圆周角定理得到∠AOD=45°,根据等腰三角形的性质得到∠ODA=∠OAD,求得∠ADP=$\frac{1}{2}∠$CAD=22.5°,得到∠ODP=∠ODA+∠ADP=90°,于是得到结论.
解答 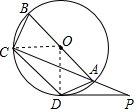 解:(Ⅰ)连接OC,OD,
解:(Ⅰ)连接OC,OD,
∵∠COD=2∠CAD,∠CAD=45°,
∴∠COD=90°,
∵AB=4,
∴OC=$\frac{1}{2}$AB=2,
∴$\widehat{CD}$的长=$\frac{90}{180}$×π×2=π;
(Ⅱ)∵$\widehat{BC}$=$\widehat{AD}$,
∴∠BOC=∠AOD,
∵∠COD=90°,
∴∠AOD=45°,
∵OA=OD,
∴∠ODA=∠OAD,
∵∠AOD+∠ODA=∠OAD=180°,
∴∠ODA=67.5°,
∵AD=AP,
∴∠ADP=∠APD,
∵∠CAD=∠ADP+∠APD,∠CAD=45°,
∴∠ADP=$\frac{1}{2}∠$CAD=22.5°,
∴∠ODP=∠ODA+∠ADP=90°,
∴PD是⊙O的切线.
点评 本题考查了切线的判定,圆内接四边形的性质,弧长的计算,正确的作出辅助线是解题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
20.下列关于图形对称性的命题,正确的是( )
| A. | 圆既是轴对称图形,又是中心对称图形 | |
| B. | 正三角形既是轴对称图形,又是中心对称图形 | |
| C. | 线段是轴对称图形,但不是中心对称图形 | |
| D. | 菱形是中心对称图形,但不是轴对称图形 |
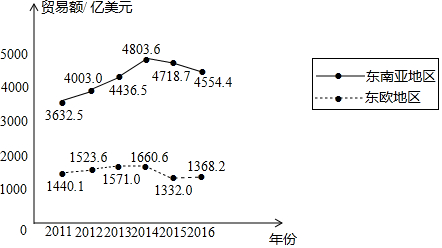
14.下面的统计图反映了我国与“一带一路”沿线部分地区的贸易情况.
2011-2016年我国与东南亚地区和东欧地区的贸易额统计图
(以上数据摘自《“一带一路”贸易合作大数据报告(2017)》)
根据统计图提供的信息,下列推断不合理的是( )
2011-2016年我国与东南亚地区和东欧地区的贸易额统计图

(以上数据摘自《“一带一路”贸易合作大数据报告(2017)》)
根据统计图提供的信息,下列推断不合理的是( )
| A. | 与2015年相比,2016年我国与东欧地区的贸易额有所增长 | |
| B. | 2011-2016年,我国与东南亚地区的贸易额逐年增长 | |
| C. | 2011-2016年,我国与东南亚地区的贸易额的平均值超过4200亿美元 | |
| D. | 2016年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的3倍还多 |
15.不等式组$\left\{\begin{array}{l}{3-2x<5}\\{x-2<1}\end{array}\right.$的解集为( )
| A. | x>-1 | B. | x<3 | C. | x<-1或x>3 | D. | -1<x<3 |
 如图,直线a∥b,Rt△ABC的顶点B在直线a上,∠C=90°,∠β=55°,求∠α的度数.
如图,直线a∥b,Rt△ABC的顶点B在直线a上,∠C=90°,∠β=55°,求∠α的度数.