题目内容
11.满足一元一次不等式组$\left\{\begin{array}{l}{x+2>1}\\{x≤1}\end{array}\right.$的整数解是x=0或x=1.分析 根据解不等式组的方法可以求得原不等式组的解集,从而可以求得满足不等式组的整数解.
解答 解:$\left\{\begin{array}{l}{x+2>1}&{①}\\{x≤1}&{②}\end{array}\right.$,
由不等式①,得
x>-1,
由不等式②,得
x≤1,
故原不等式组的解集是-1<x≤1,
∴满足一元一次不等式组$\left\{\begin{array}{l}{x+2>1}\\{x≤1}\end{array}\right.$的整数解是x=0或x=1,
故答案为:x=0或x=1.
点评 本题考查一元一次不等式组的整数解,解答本题的关键是明确解一元一次不等式组的方法.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
16.下列四组选项中,组内两个数都为无理数的是( )
| A. | $\frac{22}{7}$,$\sqrt{6}$ | |
| B. | $\frac{π}{5}$,1.010010001…(两个“1”之间依次多一个“0”) | |
| C. | $\sqrt{4}$,3.14159 | |
| D. | 2π,$-\root{3}{27}$ |
3.如表所示,请分别写出字母A、B、C、D所表示的数值,并求其中最大与最小的两个数的和.
| 字母 | 所表示的数 | 字母 | 所表示的数 |
| A | $\sqrt{5}$的相反数 | C | 整式$\frac{-{a}^{2}b}{2}$的系数 |
| B | $\frac{25}{49}$的平方根 | D | 1-$\sqrt{5}$的绝对值 |




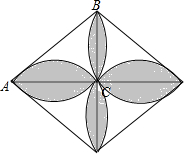 已知,在直角三角形ABC中,∠ACB=90°,AC=8,BC=6,AB=10,以AB边为直径作半圆,把4个相同的直角三角形通过一定的图形运动拼成四叶草的形状(如图所示),求阴影部分的面积.
已知,在直角三角形ABC中,∠ACB=90°,AC=8,BC=6,AB=10,以AB边为直径作半圆,把4个相同的直角三角形通过一定的图形运动拼成四叶草的形状(如图所示),求阴影部分的面积.