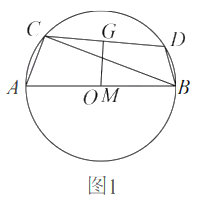Question

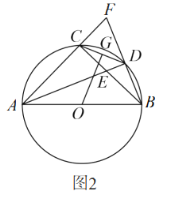
【题目】如图，已知直线与⊙相离．于点，交⊙于点，，与⊙相切于点，的延长线交直线于点．

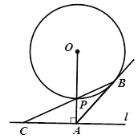
（1）求证：；

（2）若，求⊙的半径．

Answer 1

【答案】（1）见解析；（2）⊙O的半径是3．

【解析】

（1）连接OB，根据切线的性质和垂直得出∠OBA＝∠OAC＝90°，推出∠OBP＋∠ABP＝90°，∠ACP＋∠CPA＝90°，求出∠ACP＝∠ABC，根据等腰三角形的判定推出即可；
（2）设圆半径为r，则OP＝OB＝r，PA＝5r，根据AB＝AC推出，求出r即可．

⑴证明： 连接OB，

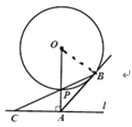
∵AB切⊙O于B，OA⊥AC，

∴∠OBA =∠OAC=90°，

∴∠OBP +∠ABP =90°，∠ACP +∠CPA =90°，

∵OP =OB， ∴∠OBP =∠OP B．

∵∠OPB =∠APC， ∴∠ACP =∠ABC，

∴AB =AC．

（2）如上图，设圆半径为，则由得，．

又∵，∴，

∵由（1）知，∴，

解得：，

即⊙O的半径是3．