МвДҝДЪИЭ
ЎҫМвДҝЎҝФД¶БІДБПЈәёчАа·ҪіМөДҪв·Ё
ЗуҪвТ»ФӘТ»ҙО·ҪіМЈ¬ёщҫЭөИКҪөД»щұҫРФЦКЈ¬°С·ҪіМЧӘ»ҜОӘx=aөДРОКҪЈ®ЗуҪв¶юФӘТ»ҙО·ҪіМЧйЈ¬°СЛьЧӘ»ҜОӘТ»ФӘТ»ҙО·ҪіМАҙҪвЈ»АаЛЖөДЈ¬ЗуҪвИэФӘТ»ҙО·ҪіМЧйЈ¬°СЛьЧӘ»ҜОӘҪв¶юФӘТ»ҙО·ҪіМЧйЈ®ЗуҪвТ»ФӘ¶юҙО·ҪіМЈ¬°СЛьЧӘ»ҜОӘБҪёцТ»ФӘТ»ҙО·ҪіМАҙҪвЈ®ЗуҪв·ЦКҪ·ҪіМЈ¬°СЛьЧӘ»ҜОӘХыКҪ·ҪіМАҙҪвЈ¬УЙУЪЎ°ИҘ·ЦДёЎұҝЙДЬІъЙъФцёщЈ¬ЛщТФҪв·ЦКҪ·ҪіМұШРлјмСйЈ®ёчАа·ҪіМөДҪв·ЁІ»ҫЎПаН¬Ј¬ө«КЗЛьГЗУРТ»ёц№ІН¬өД»щұҫКэС§ЛјПл![]() ЧӘ»ҜЈ¬°СОҙЦӘЧӘ»ҜОӘТСЦӘЈ®
ЧӘ»ҜЈ¬°СОҙЦӘЧӘ»ҜОӘТСЦӘЈ®
УГЎ°ЧӘ»ҜЎұөДКэС§ЛјПлЈ¬ОТГЗ»№ҝЙТФҪвТ»Р©РВөД·ҪіМЈ®АэИзЈ¬Т»ФӘИэҙО·ҪіМx3+x2-2x=0Ј¬ҝЙТФНЁ№эТтКҪ·ЦҪв°СЛьЧӘ»ҜОӘx(x2+x-2)=0Ј¬Ҫв·ҪіМx=0әНx2+x-2=0Ј¬ҝЙөГ·ҪіМx3+x2-2x=0өДҪвЈ®
ЈЁ1Ј©ОКМвЈә·ҪіМx3+x2-2x=0өДҪвКЗx1=0,x2= Ј¬x3= Ј»
ЈЁ2Ј©НШХ№ЈәУГЎ°ЧӘ»ҜЎұЛјПлЗу·ҪіМ![]() өДҪвЈ»
өДҪвЈ»
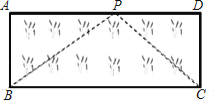
ЈЁ3Ј©УҰУГЈәИзНјЈ¬ТСЦӘҫШРОІЭЖәABCDөДіӨAD=8mЈ¬ҝнAB=3mЈ¬РЎ»Ә°СТ»ёщіӨОӘ10mөДЙюЧУөДТ»¶Л№М¶ЁФЪөгBЈ¬СШІЭЖәұЯСШBAЈ¬ADЧЯөҪөгPҙҰЈ¬°СіӨЙюPB¶ОАӯЦұІў№М¶ЁФЪөгPЈ¬И»әуСШІЭЖәұЯСШPDЎўDCЧЯөҪөгCҙҰЈ¬°СіӨЙюКЈПВөДТ»¶ОАӯЦұЈ¬іӨЙюөДБнТ»¶ЛЗЎәГВдФЪөгCЈ®ЗуAPөДіӨЈ®
Ўҫҙр°ёЎҝ(1)-2Ј¬1Ј»ЈЁ2Ј©x=3Ј»ЈЁ3Ј©4m.
ЎҫҪвОцЎҝ
ЈЁ1Ј©ТтКҪ·ЦҪв¶аПоКҪЈ¬И»әуөГҪбВЫЈ»
ЈЁ2Ј©БҪұЯЖҪ·ҪЈ¬°СОЮАн·ҪіМЧӘ»ҜОӘХыКҪ·ҪіМЈ¬ЗуҪвЈ¬ЧўТвСйёщЈ»
ЈЁ3Ј©ЙиAPөДіӨОӘxmЈ¬ёщҫЭ№ҙ№Й¶ЁАнәНBP+CP=10Ј¬ҝЙБРіц·ҪіМЈ¬УЙУЪ·ҪіМә¬УРёщәЕЈ¬БҪұЯЖҪ·ҪЈ¬°СОЮАн·ҪіМЧӘ»ҜОӘХыКҪ·ҪіМЈ¬ЗуҪвЈ¬
ҪвЈәЈЁ1Ј©![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]()
ЛщТФ![]() »т
»т![]() »т
»т![]()
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј»
Ј»
№Кҙр°ёОӘЈә![]() Ј¬1Ј»
Ј¬1Ј»
ЈЁ2Ј©![]() Ј¬
Ј¬
·ҪіМөДБҪұЯЖҪ·ҪЈ¬өГ![]()
јҙ![]()
![]()
![]() »т
»т![]()
![]() Ј¬
Ј¬![]() Ј¬
Ј¬
өұ![]() КұЈ¬
КұЈ¬![]() Ј¬
Ј¬
ЛщТФ![]() І»КЗФӯ·ҪіМөДҪвЈ®
І»КЗФӯ·ҪіМөДҪвЈ®
ЛщТФ·ҪіМ![]() өДҪвКЗ
өДҪвКЗ![]() Ј»
Ј»
ЈЁ3Ј©ТтОӘЛДұЯРО![]() КЗҫШРОЈ¬
КЗҫШРОЈ¬
ЛщТФ![]() Ј¬
Ј¬![]()
Йи![]() Ј¬Фт
Ј¬Фт![]()
ТтОӘ![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]()
![]()
![]()
![]()
![]()
БҪұЯЖҪ·ҪЈ¬өГ![]()
ХыАнЈ¬өГ![]()
БҪұЯЖҪ·ҪІўХыАнЈ¬өГ![]()
јҙ![]()
ЛщТФ![]() Ј®
Ј®
ҫӯјмСйЈ¬![]() КЗ·ҪіМөДҪвЈ®
КЗ·ҪіМөДҪвЈ®
ҙрЈә![]() өДіӨОӘ
өДіӨОӘ![]() Ј®
Ј®