题目内容
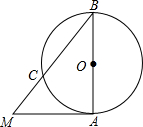已知：在⊙O中，AB是直径，AM与⊙O相切于点A，连接BM交⊙O于点C，若AM=6，半径为4，求BC的长．考点：切线的性质
专题：
分析：根据题意首先连接AC，根据切线的性质和圆周角定理的推论，经判断得到两个直角三角形；然后借助勾股定理及射影定理即可解决问题．
解答：
解：连接AC；
∵AM与⊙O相切于点A，AB是直径，
∴AB⊥AM，AC⊥BM；
又∵⊙O的半径为4，
∴AB=8；
由勾股定理得：BM=
=
=10；
由射影定理得：AB2=BC•BM，
∴BC=
=
=6.4，
即BC的长为6.4．
解：连接AC；∵AM与⊙O相切于点A，AB是直径，
∴AB⊥AM，AC⊥BM；
又∵⊙O的半径为4，
∴AB=8；
由勾股定理得：BM=
| 82+62 |
| 100 |
由射影定理得：AB2=BC•BM，
∴BC=
| AB2 |
| BM |
| 64 |
| 10 |
即BC的长为6.4．
点评：该题主要考查了切线的性质定理及其应用问题；同时还渗透了对勾股定理及射影定理的考查；对综合分析问题解决问题的能力提出了较高的要求．
练习册系列答案
相关题目
某公园草坪的防护栏由100段形状相同的抛物线形构件组成，为了牢固起见，每段护栏需间距0.4m加设一根不锈钢的支柱，防护栏的最高点距底部0.5m（如图所示），请计算所需不锈钢立柱的总长度．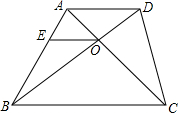
如图，在梯形ABCD中，AD∥BC，对角线AC与BD相交于点O，过点O作OE∥AD交AB于点E．若AD=6cm，BC=12cm，△AOD的面积为6cm2，
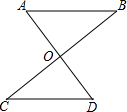已知：如图，AD与BC相交于点O，OA=OD，OB=OC．求证：
如图，梯形ABCD中，若DC∥AB，AD=BC，∠A=60°，BD⊥AD，那么∠DBA=