题目内容
 如图,梯形ABCD中,若DC∥AB,AD=BC,∠A=60°,BD⊥AD,那么∠DBA=
如图,梯形ABCD中,若DC∥AB,AD=BC,∠A=60°,BD⊥AD,那么∠DBA=考点:梯形
专题:
分析:先根据直角三角形的性质求出∠DAB的度数,再由DC∥AB,AD=BC判断出梯形ABCD是等腰梯形,故∠C=∠ADC,由此可得出结论.
解答:解:∵△ABD中,BD⊥AD,∠A=50°,
∴∠ADB=90°,
∴∠DBA=90°-60°=30°.
∵梯形ABCD中,DC∥AB,AD=BC,∠A=60°,
∴梯形ABCD是等腰梯形,
∴∠C=∠ADC=180°-60°=120°.
故答案为:30,120.
∴∠ADB=90°,
∴∠DBA=90°-60°=30°.
∵梯形ABCD中,DC∥AB,AD=BC,∠A=60°,
∴梯形ABCD是等腰梯形,
∴∠C=∠ADC=180°-60°=120°.
故答案为:30,120.
点评:本题考查的是梯形,熟知等腰梯形的性质是解答此题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
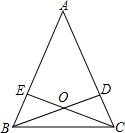 如图,已知AB=AC,AE=AD,则①△ABD≌△ACE,②△BOE≌△COD,③点O在∠BAC的平分线上,( )
如图,已知AB=AC,AE=AD,则①△ABD≌△ACE,②△BOE≌△COD,③点O在∠BAC的平分线上,( )| A、都正确 |
| B、都不正确 |
| C、只有一个正确 |
| D、只有一个不正确 |
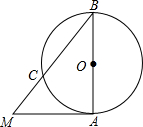 已知:在⊙O中,AB是直径,AM与⊙O相切于点A,连接BM交⊙O于点C,若AM=6,半径为4,求BC的长.
已知:在⊙O中,AB是直径,AM与⊙O相切于点A,连接BM交⊙O于点C,若AM=6,半径为4,求BC的长. 如图△ABC中,AD⊥BC于D,AE为∠A的平分线,已知∠B=30°,∠C=50°,求∠BAE和∠DAE的度数.
如图△ABC中,AD⊥BC于D,AE为∠A的平分线,已知∠B=30°,∠C=50°,求∠BAE和∠DAE的度数. 如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是
如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是