题目内容
14. 如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE=( )
如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE=( )| A. | 2 | B. | 3 | C. | 4.5 | D. | 6 |
分析 根据位似图形的性质得出AO,DO的长,进而得出 $\frac{AO}{DO}$=$\frac{AB}{DE}$=$\frac{1}{3}$,求出DE的长即可.
解答 解:∵△ABC与DEF是位似图形,它们的位似中心恰好为原点,已知A点坐标为(1,0),D点坐标为(3,0),
∴AO=1,DO=3,
∴$\frac{AO}{DO}$=$\frac{AB}{DE}$=$\frac{1}{3}$,
∵AB=1.5,
∴DE=4.5.
故答案为:4.5.
点评 此题主要考查了位似图形的性质以及坐标与图形的性质,根据已知点的坐标得出 $\frac{AO}{DO}$=$\frac{AB}{DE}$=$\frac{1}{3}$ 是解题关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
4.取一次函数y=kx+b部分的自变量x值和对应函数y值如表:
根据信息,下列说法错误的是( )
| x | … | -1 | 0 | 1 | … |
| y | … | -3 | -1 | 1 | … |
| A. | -k+b=-3 | B. | 当x<1时y<1 | ||
| C. | k+b=-1 | D. | 不等式kx+b>-1的解集是x>0 |
5.在我市开展的“好书伴我成长”读书活动中,学校随机调查了九年级50名学生度数的册数统计数据如下表所示:
那么这50名学生读书册数的平均数与中位数分别为( )
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 3 | 13 | 16 | 17 | 1 |
| A. | 2和3 | B. | 3和3 | C. | 2和2 | D. | 3和2 |
2.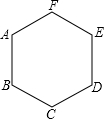 如图,已知正六边形ABCDEF的边长为5cm,一只电子蚂蚁从顶点A出发沿着正六边形的边爬行,当爬行50cm时,电子蚂蚁离A点的距离为 ( )
如图,已知正六边形ABCDEF的边长为5cm,一只电子蚂蚁从顶点A出发沿着正六边形的边爬行,当爬行50cm时,电子蚂蚁离A点的距离为 ( )
 如图,已知正六边形ABCDEF的边长为5cm,一只电子蚂蚁从顶点A出发沿着正六边形的边爬行,当爬行50cm时,电子蚂蚁离A点的距离为 ( )
如图,已知正六边形ABCDEF的边长为5cm,一只电子蚂蚁从顶点A出发沿着正六边形的边爬行,当爬行50cm时,电子蚂蚁离A点的距离为 ( )| A. | $5\sqrt{2}$cm | B. | $5{\sqrt{3}^{\;}}$cm | C. | 5(1+$\sqrt{2}$)cm | D. | 5(1+$\sqrt{3}$)cm |
9.若点A(2,3)、B(a-1,-2)都在函数y=$\frac{k}{x}$的图象上,则a的值是( )
| A. | 3 | B. | 2 | C. | -3 | D. | -2 |
19.函数y=$\frac{k}{x}$的图象经过点A(1,-5),则k的值为( )
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | 5 | D. | -5 |
6.下列算式中,运算结果为负数的是( )
| A. | (-2017)2 | B. | -(-2017) | C. | -|-2017| | D. | 2017-2 |
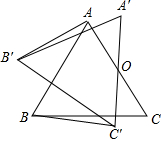 已知:如图,等边三角形△ABC,O为AC边的中点,将△ABC绕点O顺时针旋转α角(0°<α<90°)到△A′B′C′的位置,连接AB′,BC′.
已知:如图,等边三角形△ABC,O为AC边的中点,将△ABC绕点O顺时针旋转α角(0°<α<90°)到△A′B′C′的位置,连接AB′,BC′.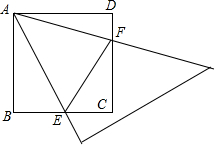 如图,将一把含45°角的三角尺,放在正方形ABCD上,三角尺绕着顶点A转动时,与正方形的BC、CD两边分别交于点E、F.
如图,将一把含45°角的三角尺,放在正方形ABCD上,三角尺绕着顶点A转动时,与正方形的BC、CD两边分别交于点E、F.