题目内容
两直线y=x+3和y=-2x+6与x轴所围成的面积为 .
考点:一次函数图象上点的坐标特征
专题:
分析:先求出直线y=x+3和y=-2x+6的交点坐标,再分别求出直线与x轴的交点,利用三角形的面积公式即可得出结论.
解答:解:∵
,解得
,
∴直线y=x+3和y=-2x+6的交点坐标为(1,4),
∵直线y=x+3与x轴的交点坐标为(-3,0),直线y=-2x+6与x轴的交点坐标为(3,0),
∴两直线与x轴所围成的面积=
×4×|-3-3|=2×6=12.
故答案为:12.
|
|
∴直线y=x+3和y=-2x+6的交点坐标为(1,4),
∵直线y=x+3与x轴的交点坐标为(-3,0),直线y=-2x+6与x轴的交点坐标为(3,0),
∴两直线与x轴所围成的面积=
| 1 |
| 2 |
故答案为:12.
点评:本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知等腰三角形的一边长为4cm,另一边长为5cm,则三角形的周长为( )
| A、14cm |
| B、13cm |
| C、13cm或14cm |
| D、18cm |
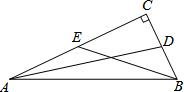 如图在△ABC中,D、E分别是BC、AC的中点.∠ACB=90°,BE=4,AD=7,则AB的长为
如图在△ABC中,D、E分别是BC、AC的中点.∠ACB=90°,BE=4,AD=7,则AB的长为 如图,已知在梯形ABCD中,AD∥BC,AB=DC=3,P是BC上一动点,PE∥AB交AC于点E,PF∥CD交BD于点F,则PE+PF=
如图,已知在梯形ABCD中,AD∥BC,AB=DC=3,P是BC上一动点,PE∥AB交AC于点E,PF∥CD交BD于点F,则PE+PF=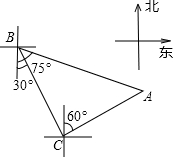 轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在观测灯塔A北偏东60°方向上,则C处与灯塔A的距离是
轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在观测灯塔A北偏东60°方向上,则C处与灯塔A的距离是