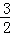题目内容
已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连接FD交AC于点E.
(1)求 的值;
的值;
(2)若AB=a,FB=EC,求AC的长.

考点: 三角形中位线定理;平行线分线段成比例;相似三角形的判定与性质.
专题: 几何综合题.
分析: (1)过点F作FM∥AC,交BC于点M.根据平行线分线段成比例定理分别找到AE,CE与FM之间的关系,得到它们的比值;
(2)结合(1)中的线段之间的关系,进行求解.
解答: 解:(1)过点F作FM∥AC,交BC于点M,
∵F为AB的中点,
∴M为BC的中点,FM= AC.
AC.
∵FM∥AC,
∴∠CED=∠MFD,∠ECD=∠FMD.
∴△FMD∽△ECD.
∴ .
.
∴EC= FM=
FM= ×
× AC=
AC= AC.
AC.
∴ .
.
(2)∵AB=a,
∴FB= AB=
AB= a.
a.
∵FB=EC,
∴EC= a.
a.
∵EC= AC,
AC,
∴AC=3EC= a.
a.

点评: 此类题要注意作平行线,能够根据平行线分线段成比例定理和相似三角形对应边成比例即可求得线段的比.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 的图象(请画图)回答问题:当函数值为正时,x的取值范围是
的图象(请画图)回答问题:当函数值为正时,x的取值范围是 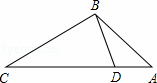
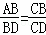 D.
D. 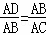
 ,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).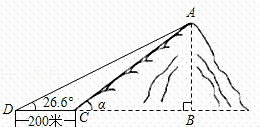
 B.
B.  C.
C.  D. 1
D. 1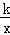 (k≠0)在第一象限内的图象经过点D、E,且D点的横坐标是它的纵坐标的2倍.
(k≠0)在第一象限内的图象经过点D、E,且D点的横坐标是它的纵坐标的2倍.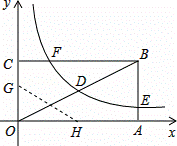
 的图象大致如图.若y1<y2,则自变量x的取值范围是( )
的图象大致如图.若y1<y2,则自变量x的取值范围是( )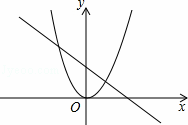
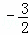 <x<2 B. x>2或x<
<x<2 B. x>2或x<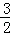 D. x<﹣2或x>
D. x<﹣2或x>