题目内容
2.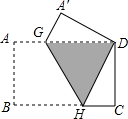 已知矩形纸片ABCD中,AB<BC,AB=4.将它沿GH折叠,如图,使点B与点D重合.当折叠后纸片重叠部分(即图中阴影部分)的面积占矩形纸片面积的$\frac{5}{16}$时,则BC的长为8.
已知矩形纸片ABCD中,AB<BC,AB=4.将它沿GH折叠,如图,使点B与点D重合.当折叠后纸片重叠部分(即图中阴影部分)的面积占矩形纸片面积的$\frac{5}{16}$时,则BC的长为8.
分析 由折叠的性质得出A′G=AG,A′D=AB=4,∠A′=∠A=90°,设AD=BC=x,DG=y,则A′G=AG=x-y,由面积关系和勾股定理得出方程组,解方程组即可.
解答 解:由折叠的性质得:A′G=AG,A′D=AB=4,∠A′=∠A=90°,
设AD=BC=x,DG=y,则A′G=AG=x-y,
根据题意得:$\left\{\begin{array}{l}{\frac{5}{16}x×4x=\frac{1}{2}×4y}\\{{4}^{2}+(x-y)^{2}={y}^{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=8}\\{y=5}\end{array}\right.$,
即BC的长为8;
故答案为:8.
点评 本题考查了矩形的性质、翻折变换的性质、勾股定理、三角形的面积关系;熟练掌握翻折变换的性质,根据面积关系和勾股定理得出方程组是解决问题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
10.据统计,怀柔雁栖湖常年总库容量38300000立方米,将38300000用科学记数法表示为( )
| A. | 0.383×108 | B. | 3.83×107 | C. | 38.3×106 | D. | 383×105 |
14.将5a,$\frac{6}{{2{a^2}b}},\frac{a}{{4{b^3}}}$通分后最简公分母是( )
| A. | 8a2b3 | B. | 4ab3 | C. | 8a2b4 | D. | 4a2b3 |

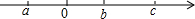 有理数a、b、c在数轴上的位置如图.
有理数a、b、c在数轴上的位置如图. 桌面上放着1个长方体和1个圆柱体,按如图所示的方式摆放在一起,不是其三视图的是( )
桌面上放着1个长方体和1个圆柱体,按如图所示的方式摆放在一起,不是其三视图的是( )


