题目内容
10.如图,已知A、B、C是数轴上三点,点C表示的数为3,BC=2,AB=6.
(1)数轴上点A表示的数为-5,B表示的数为1;
(2)动点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒1个单位长度的速度沿数轴向左匀速运动,M为AP的中点,点N在线段CQ上,且CN=$\frac{2}{3}$CQ,设运动时间t(t>0)秒.
①求数轴上M、N表示的数(用含t的式子表示);
②t为何值时,原点O恰好是线段PQ的中点.
分析 (1)根据点C所表示的数,以及BC、AB的长度,即可写出点A、B表示的数;
(2)①根据题意画出图形,表示出AP=6t,CQ=3t,再根据线段的中点定义可得AM=3t,根据线段之间的和差关系进而可得到点M表示的数;根据CN=$\frac{2}{3}$CQ可得CN=t,根据线段的和差关系可得到点N表示的数;
②此题有两种情况:当点P在点O的左侧,点Q在点O的右侧时;当P在点O的右侧,点Q在点O的左侧时,分别画出图形进行计算即可.
解答 解:(1)∵C表示的数为3,BC=2,
∴OB=3-2=1,
∴B点表示1.
∵AB=6,
∴AO=6-1=5,
∴A点表示-5.
故答案为:-5,1;
(2)①由题意得:AP=2t,CQ=t,如图1所示:
∵M为AP中点,
∴AM=$\frac{1}{2}$AP=t,
∴在数轴上点M表示的数是-5+t,
∵点N在CQ上,CN=$\frac{2}{3}$CQ,
∴CN=$\frac{2}{3}$t,
∴在数轴上点N表示的数是3-$\frac{2}{3}$t;
②由题意得,AP=2t,CQ=t,分两种情况:
i)如图2所示:当点P在点O的左侧,点Q在点O的右侧时,OP=5-2t,OQ=3-t,
∵O为PQ的中点,
∴OP=OQ,
∴5-2t=3-t,
解得:t=2.
当t=2秒时,O为PQ的中点;
ii)如图3所示:当P在点O的右侧,点Q在点O的左侧时,OP=2t-5,OQ=t-3,
∵O为PQ的中点,
∴OP=OQ,
∴2t-5=t-3,
解得:t=2,
此时AP=4<5,
∴t=2不合题意舍去.
综上所述:当t=2秒时,O为PQ的中点.
点评 此题主要考查了一元一次方程的应用、数轴,以及线段的计算,解决问题的关键是根据题意正确画出图形,要考虑全面各种情况,不要漏解.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
6.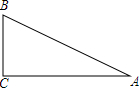 如图,在直角△ABC中,∠C=90°,BC=1,tanA=$\frac{1}{2}$,下列判断正确的是( )
如图,在直角△ABC中,∠C=90°,BC=1,tanA=$\frac{1}{2}$,下列判断正确的是( )
 如图,在直角△ABC中,∠C=90°,BC=1,tanA=$\frac{1}{2}$,下列判断正确的是( )
如图,在直角△ABC中,∠C=90°,BC=1,tanA=$\frac{1}{2}$,下列判断正确的是( )| A. | ∠A=30° | B. | AC=$\frac{1}{2}$ | C. | AB=2 | D. | AC=2 |
 如图,AB=AC,D、E分别在AC、AB上,要使△ABD≌△ACE,则还需要添加的一个条件是∠B=∠C(答案不唯一)(填写一个条件即可).
如图,AB=AC,D、E分别在AC、AB上,要使△ABD≌△ACE,则还需要添加的一个条件是∠B=∠C(答案不唯一)(填写一个条件即可).
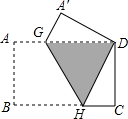 已知矩形纸片ABCD中,AB<BC,AB=4.将它沿GH折叠,如图,使点B与点D重合.当折叠后纸片重叠部分(即图中阴影部分)的面积占矩形纸片面积的$\frac{5}{16}$时,则BC的长为8.
已知矩形纸片ABCD中,AB<BC,AB=4.将它沿GH折叠,如图,使点B与点D重合.当折叠后纸片重叠部分(即图中阴影部分)的面积占矩形纸片面积的$\frac{5}{16}$时,则BC的长为8.