题目内容
3.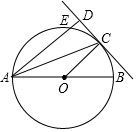 如图,AB是⊙O的直径,点C为⊙O上一点,AD和过C点切线交于点D,和⊙O相交于E,且AC平分∠DAB.
如图,AB是⊙O的直径,点C为⊙O上一点,AD和过C点切线交于点D,和⊙O相交于E,且AC平分∠DAB.(1)求证:∠ADC=90°;
(2)若AB=10,AD=8,求CD的长.
分析 (1)由OA=OC知∠OAC=∠OCA,由AC平分∠DAB知∠DAC=∠OAC,从而得∠OCA=∠DAC,即可知AD∥OC,根据⊙O与CD相切,即∠OCD=90°可得∠ADC=180°-∠OCD=90°;
(2)作OF⊥AD,可知∠OFD=∠OCD=∠CDA=90°,得四边形OCFD是矩形,即可知OC=DF=$\frac{1}{2}$AB=5、CD=OF,根据勾股定理得OF=CD=4.
解答 解:(1)∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴∠OCA=∠DAC,
∴AD∥OC,
又∵⊙O与CD相切,
∴∠OCD=90°,
∴∠ADC=180°-∠OCD=90°;
(2)过点O作OF⊥AD于点F,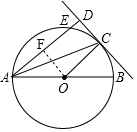
则∠OFD=∠OCD=∠CDA=90°,
∴四边形OCFD是矩形,
∴OC=DF=$\frac{1}{2}$AB=5,CD=OF,
在Rt△OFA中,∵OA=5,AF=AD-DF=8-5=3,
∴OF=$\sqrt{O{A}^{2}-A{F}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴CD=4.
点评 本题主要考查圆的基本性质、切线的性质、平行线的判定与性质、矩形的判定与性质及勾股定理,熟练掌握圆的基本性质和切线的性质是解题的关键'.

练习册系列答案
相关题目
14.在一个不透明的袋中装着3个红球和1个黄球,它们只有颜色上的区别,随机从袋中摸出两个小球,两球恰好是一个黄球和一个红球的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
 如图,将长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′处,若∠AFE=68°,则∠C′EF=68°.
如图,将长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′处,若∠AFE=68°,则∠C′EF=68°.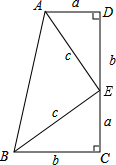 如图,已知∠C=∠D=90°,D,E,C三点共线,各边长如图所示,请利用面积法证明勾股定理.
如图,已知∠C=∠D=90°,D,E,C三点共线,各边长如图所示,请利用面积法证明勾股定理.