题目内容
19.如图,直角△ABC,∠B=30°.(1)过A点作一条直线AD交BC于D点,使S△ABD=2S△ACD,并说明理由;
(2)在图(2)中,作二条直线将△ABC分成三个三角形,使三个三角形均为全等三角形,并作简单证明(要求:尺规作图,不写作法,保留作图痕迹).
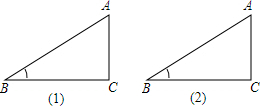
分析 (1)要使S△ABD=2S△ACD,只要在BC上找到点D使BD=2CD,连接AD即可;利用高相等的三角形,底之比等于面积比得出答案;
(2)作AB的垂直平分线,分别交AB、BC于点D、E,连接AE即可根据线段垂直平分线的性质可得将△ABC分成三个三角形,使三个三角形均为全等三角形;进一步利用三角形全等的判定方法证明△ADE≌△DBE,△DBE≌△CAE得出答案即可.
解答 解:(1)如图,在BC上找到点D使BD=2CD,连接AD.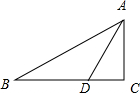
S△ABD=$\frac{1}{2}$BD•AC,S△ACD=$\frac{1}{2}$DC•AC,
∵BD=2CD,
∴S△ABD=2S△ACD.
(2)如图,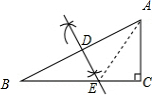
∵DE是AB的垂直平分线,
∴AE=EB,AD=DB,
∴∠A=∠BAE=30°,
∴∠AEC=60°,
∵∠C=90°,
∴∠EAC=30°
在△BDE和△ADE中,
$\left\{\begin{array}{l}{BD=AD}\\{DE=DE}\\{BE=AE}\end{array}\right.$,
∴△BDE≌△ADE(SSS),
在△ADE和△ACE中,
$\left\{\begin{array}{l}{∠DEA=∠C}\\{∠DAE=∠CAE}\\{EA=EA}\end{array}\right.$,
∴△DAE≌△CAE(AAS),
∴△BDE≌△ACE≌△DAE.
点评 此题考查作图-应用与设计作图,全等三角形的判定,掌握三角形的面积,垂直平分形的性质以及全等三角形的判定是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.下列式子是最简二次根式的是( )
| A. | $\sqrt{18}$ | B. | $\sqrt{24}$ | C. | $\sqrt{0.5}$ | D. | $\sqrt{6}$ |
11.已知两个三角形相似,对应中线之比为1:4,那么对应周长之比为( )
| A. | 1:2 | B. | 1:16 | C. | 1:4 | D. | 无法确定 |
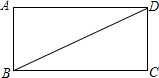 如图,矩形ABCD中,AB=4,BC=8,若以点D为圆心,DA长为半径画弧与以点B为圆心,BD长为半径画弧的交点为P,则点P到AD的距离为8或$\frac{24}{5}$.
如图,矩形ABCD中,AB=4,BC=8,若以点D为圆心,DA长为半径画弧与以点B为圆心,BD长为半径画弧的交点为P,则点P到AD的距离为8或$\frac{24}{5}$.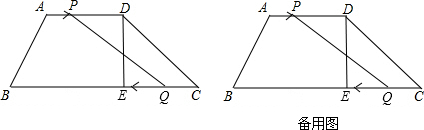
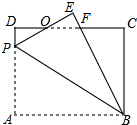 如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD.
如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD.