Question

如图，在△ABC中，AB=AC，E是BC中点，点O在AB上，以OB为半径的⊙O经过点AE上的一点M，分别交AB，BC于点F，G，连BM，此时∠FBM=∠CBM．

（1）求证：AM是⊙O的切线；

（2）当BC=6，OB：OA=1：2 时，求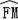，AM，AF围成的阴影部分面积．

Answer 1

【考点】切线的判定；勾股定理；扇形面积的计算；相似三角形的判定与性质．

【专题】计算题．

【分析】（1）连接OM，由AB=AC，且E为BC中点，利用三线合一得到AE垂直于BC，再由OB=OM，利用等边对等角得到一对角相等，由已知角相等，等量代换得到一对内错角相等，利用内错角相等两直线平行得到OM与BC平行，可得出OM垂直于AE，即可得证；

（2）由E为BC中点，求出BE的长，再由OB与OA的比值，以及OB=OM，得到OM与OA的比值，由OM垂直于AE，利用直角三角形中一直角边等于斜边的一半，得到此直角边所对的角为30度得到∠MAB=30°，∠MOA=60°，阴影部分的面积=三角形AOM面积﹣扇形MOF面积，求出即可．

【解答】解：（1）连结OM，

∵AB=AC，E是BC中点，

∴BC⊥AE，

∵OB=OM，

∴∠OMB=∠MBO，

∵∠FBM=∠CBM，

∴∠OMB=∠CBM，

∴OM∥BC，

∴OM⊥AE，

∴AM是⊙O的切线；

 

（2）∵E是BC中点，

∴BE=BC=3，

∵OB：OA=1：2，OB=OM，

∴OM：OA=1：2，

∵OM⊥AE，

∴∠MAB=30°，∠MOA=60°，OA：BA=1：3，

∵OM∥BC，

∴△AOM∽△ABE，

∴==，

∴OM=2，

∴AM==2，

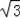
∴S_阴影=×2×2﹣=2﹣π．

【点评】此题考查了切线的判定，涉及的知识有：圆周角定理，弧，弦及圆心角之间的关系，平行线的性质，扇形面积求法，以及勾股定理，熟练掌握切线的判定方法是解本题的关键．