题目内容
8. 如图,直线AB、CD相交于点O,OE平分∠BOD.
如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数.
(2)若OF平分∠COE,∠BOF=30°,求∠AOC的度数.
分析 (1)根据对顶角相等和角平分线的定义计算即可;
(2)设∠AOC=x,根据对顶角相等和角平分线的定义用x表示出∠BOE和∠EOF,根据题意列方程,解方程即可.
解答 解:(1)∵直线AB、CD相交于点O,
∴∠BOD=∠AOC=68°,
∵OE平分∠BOD,
∴∠DOE=$\frac{1}{2}$∠BOD=34°,
∴∠EOF=∠DOF-∠DOE=56°;
(2)设∠AOC=x,则∠BOD=x,
∵OE平分∠BOD,
∴∠BOE=∠DOE=$\frac{1}{2}$x,
∵OF平分∠COE,
∴∠EOF=$\frac{1}{2}$(180°-$\frac{1}{2}$x),
由题意得,$\frac{1}{2}$(180°-$\frac{1}{2}$x)-$\frac{1}{2}$x=30°,
解得,x=80°,
∴∠AOC=80°.
点评 本题考查的是对顶角、邻补角的概念和性质,掌握对顶角相等、邻补角之和为180°以及角平分线的定义是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
19. 如图,若△ABC中,∠C=90°,AD平分∠BAC,CD=3cm,AB=10cm,则△ABD的面积是( )
如图,若△ABC中,∠C=90°,AD平分∠BAC,CD=3cm,AB=10cm,则△ABD的面积是( )
 如图,若△ABC中,∠C=90°,AD平分∠BAC,CD=3cm,AB=10cm,则△ABD的面积是( )
如图,若△ABC中,∠C=90°,AD平分∠BAC,CD=3cm,AB=10cm,则△ABD的面积是( )| A. | 15cm2 | B. | 10cm2 | C. | 5cm2 | D. | 2.5cm2 |
16.下列各组中的两个分式不相等的是( )
| A. | $\frac{2x}{y}$与$\frac{4xy}{{2y}^{2}}$ | B. | $\frac{-2{mn}^{2}}{{4m}^{2}n}$与-$\frac{n}{2m}$ | ||
| C. | $\frac{-5y}{-2{5x}^{2}}$与$\frac{y}{{5x}^{2}}$ | D. | $\frac{{y}^{2}-{x}^{2}}{{(x-y)}^{2}}$与$\frac{x+y}{x-y}$ |
13.下列方程中,一元二次方程共有( )个
①x2-2x-1=0;②ax2+bx+c=0;③$\frac{1}{{x}^{2}}$+3x-5=0;④-x2=0;⑤(x-1)2+y2=2;⑥(x-1)(x-3)=x2.
①x2-2x-1=0;②ax2+bx+c=0;③$\frac{1}{{x}^{2}}$+3x-5=0;④-x2=0;⑤(x-1)2+y2=2;⑥(x-1)(x-3)=x2.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.据统计部门预测,到2020年武汉市常住人口将达到约14500000人,数字14500000用科学记数法表示为( )
| A. | 0.145×108 | B. | 1.45×107 | C. | 14.5×106 | D. | 145×105 |
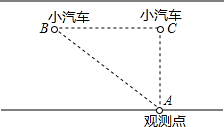 “中华人民共和国道路交通管理条例”规定:小汽车在沿海高速路(盐城到上海段)上的行驶速度不能低于$\frac{50}{3}$米/秒不得超过$\frac{100}{3}$米/秒,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方60米处,过了3秒后,测得小汽车与车速检测仪问的距离变为100米.这辆小汽车行驶速速度符合规定吗?(①符合;②不符合)符合.
“中华人民共和国道路交通管理条例”规定:小汽车在沿海高速路(盐城到上海段)上的行驶速度不能低于$\frac{50}{3}$米/秒不得超过$\frac{100}{3}$米/秒,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方60米处,过了3秒后,测得小汽车与车速检测仪问的距离变为100米.这辆小汽车行驶速速度符合规定吗?(①符合;②不符合)符合.