题目内容
19. 如图,若△ABC中,∠C=90°,AD平分∠BAC,CD=3cm,AB=10cm,则△ABD的面积是( )
如图,若△ABC中,∠C=90°,AD平分∠BAC,CD=3cm,AB=10cm,则△ABD的面积是( )| A. | 15cm2 | B. | 10cm2 | C. | 5cm2 | D. | 2.5cm2 |
分析 作DE⊥AB于E,根据角的平分线上的点到角的两边的距离相等求出DE的长,根据三角形的面积公式计算即可.
解答 解: 作DE⊥AB于E,
作DE⊥AB于E,
∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DE=DC=3cm,
∴△ABD的面积=$\frac{1}{2}$×AB×DE=15cm2,
故选:A.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
7.已知甲、乙两班男、女生人数的扇形统计图如图,则下列说法正确的是( )
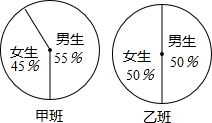

| A. | 甲班男生比乙班男生多 | B. | 乙班女生比甲班女生多 | ||
| C. | 乙班女生与乙班男生一样多 | D. | 甲、乙两班人数一样多 |
4.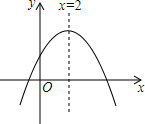 二次函数y=ax2+bx+c的图象如图所示,若点A(-1,y1),B(-2,y2)是其图象上的两点,则y1与y2的大小关系是( )
二次函数y=ax2+bx+c的图象如图所示,若点A(-1,y1),B(-2,y2)是其图象上的两点,则y1与y2的大小关系是( )
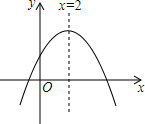 二次函数y=ax2+bx+c的图象如图所示,若点A(-1,y1),B(-2,y2)是其图象上的两点,则y1与y2的大小关系是( )
二次函数y=ax2+bx+c的图象如图所示,若点A(-1,y1),B(-2,y2)是其图象上的两点,则y1与y2的大小关系是( )| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法确定 |
11.若a:b:c=2:3:4且a+b-c=6,则a-b+c=( )
| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
9.使分式$\frac{2}{x-3}$有意义的x的取值范围是( )
| A. | x≠3 | B. | x>3 | C. | x<3 | D. | x=3 |
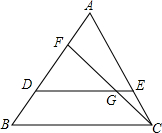 已知:如图,在△ABC中,点D.E分别在AB,AC上,DE∥BC,点F在边AB上,BC2=BF•BA,CF与DE相交于点G.
已知:如图,在△ABC中,点D.E分别在AB,AC上,DE∥BC,点F在边AB上,BC2=BF•BA,CF与DE相交于点G. 如图,直线AB、CD相交于点O,OE平分∠BOD.
如图,直线AB、CD相交于点O,OE平分∠BOD.