题目内容
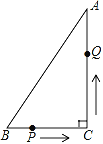
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 分别为
分别为![]() 边上的动点.
边上的动点.
(1)若点![]() 分别为
分别为![]() 的中点,求线段
的中点,求线段![]() 的长;
的长;
(2)若![]() ,
,
①求证: ![]() ∽
∽![]() ;
;
②试问![]() 与
与![]() 相似吗?并说明理由.
相似吗?并说明理由.

【答案】(1)EF=![]() ;(2)①证明见解析;②
;(2)①证明见解析;②![]() 与
与![]() 相似,理由见解析.
相似,理由见解析.
【解析】试题分析:(1)根据三角形的中位线的性质定理即可求解;
(2)由![]() ,
, ![]() 得∠A=∠B=45°,因为∠EOF=45°,所以∠BOE+∠AOF=135°,又∠BEO+∠BOE=135°,故∠BEO=∠AOF,从而可证ΔBOE∽ΔAFO;
得∠A=∠B=45°,因为∠EOF=45°,所以∠BOE+∠AOF=135°,又∠BEO+∠BOE=135°,故∠BEO=∠AOF,从而可证ΔBOE∽ΔAFO;
(3)由(2)得![]() ,因O为AB的中点得OA=OB,所以
,因O为AB的中点得OA=OB,所以![]() ,而∠B=∠EOF,故
,而∠B=∠EOF,故![]() ∽
∽![]() .
.
试题解析:(1)∵E、F分别为![]() 的中点
的中点
∴EF= ![]()
又∵![]() ,
, ![]()
∴AB=![]()
∴EF=![]()
(2) ①∵![]() ,
, ![]()
∴∠A=∠B=45°
又∵∠EOF=45°
∴∠BOE+∠AOF=135°
又∠BEO+∠BOE=135°
∴∠BEO=∠AOF
∴⊿BOE∽⊿AFO
②![]() 与
与![]() 相似,理由如下:
相似,理由如下:
由(2)得: ![]()
又∵O为AB的中点
∴OA=OB
∴![]()
又∵∠B=∠EOF
∴![]() ∽
∽![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目