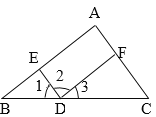
题目内容
【题目】如图①,在![]() 中,
中, ![]() ,
, ![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,连接
,连接![]() 、
、![]() .直线
.直线![]() 、
、![]() 交于点
交于点![]() .
.
(![]() )当
)当![]() 时,
时, ![]() __________.
__________.
(![]() )在旋转过程中,四边形
)在旋转过程中,四边形![]() 的面积是否存在最大值?若存在,求出最大值.若不存在,说明理由.
的面积是否存在最大值?若存在,求出最大值.若不存在,说明理由.
(![]() )如图②.若
)如图②.若![]() 中,
中, ![]() ,其余条件不变,四边形
,其余条件不变,四边形![]() 的面积是否存在最大值?若存,求出最大值.若不存在,说明理由.
的面积是否存在最大值?若存,求出最大值.若不存在,说明理由.

【答案】(1)![]() ;(
;(![]() )存在,理由见解析;(
)存在,理由见解析;(![]() )存在,理由见解析.
)存在,理由见解析.
【解析】试题分析:(1)根据等腰三角形两底角相等,即可解决问题.
(2)存在.首先证明∠AMC=90°,在Rt△ABC中,根据AB=4,BC=3,可得![]() ,可得S△ABC=
,可得S△ABC=![]() ×3×4=6,因为当△ACM的面积最大时,四边形ABCM的面积最大,因为△ACM是直角三角形,AC=5,所以当AM=CM=
×3×4=6,因为当△ACM的面积最大时,四边形ABCM的面积最大,因为△ACM是直角三角形,AC=5,所以当AM=CM=![]() 时,△ACM的面积最大,最大值为=
时,△ACM的面积最大,最大值为=![]() ,由此即可解决问题.
,由此即可解决问题.
(3)存在.如图②中,作AN⊥BC于N.首先证明∠AMC=60°,在Rt△ABN中,AB=4,∠ABN=60°,推出BN=![]() AB=2,AN=
AB=2,AN=![]() ,在Rt△ACN中,
,在Rt△ACN中, ![]() ,可得S△ABC=
,可得S△ABC=![]() ×3×2=
×3×2=![]() ,因为当△ACM的面积最大时,四边形ABCM的面积最大,因为∠AMC=60°所以当△ACM是等边三角形时,△ACM的面积最大,由此即可解决问题.
,因为当△ACM的面积最大时,四边形ABCM的面积最大,因为∠AMC=60°所以当△ACM是等边三角形时,△ACM的面积最大,由此即可解决问题.
解:(![]() )∵
)∵![]() ,
, ![]() ,
,
∴![]() .
.
故答案为![]() .
.
(![]() )存在,理由如下,
)存在,理由如下,
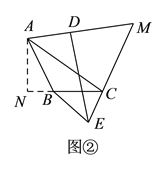
如图①中,
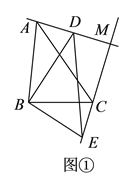
∵![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴当![]() 的面积最大时,四边形
的面积最大时,四边形![]() 的面积最大,
的面积最大,
∵![]() 是直角三角形,
是直角三角形, ![]() ,
,
∴当![]() 时,
时, ![]() 的面积最大,最大值为
的面积最大,最大值为![]() ,
,
∴四边形![]() 的面积的最大值为
的面积的最大值为![]() .
.
(![]() )存在,理由如下,
)存在,理由如下,
如图②中,作![]() 于
于![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴当![]() 的面积最大时,四边形
的面积最大时,四边形![]() 的面积最大,
的面积最大,
∵![]() ,
,
∴当![]() 是等边三角形时,
是等边三角形时, ![]() 的面积最大,
的面积最大,
最大值为![]() ,
,
∴四边形![]() 的面积的最大值为
的面积的最大值为![]() .
.

【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.
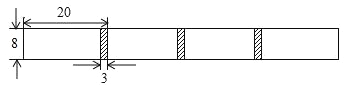
![]() 根据题意,将下面的表格补充完整:
根据题意,将下面的表格补充完整:
白纸张数 | 1 | 2 | 3 | 4 | 5 |
|
纸条长度 | 20 | ______ | 54 | 71 | ______ |
|
![]() 直接写出用x表示y的关系式:______ ;
直接写出用x表示y的关系式:______ ;
![]() 要使粘合后的总长度为1006cm,需用多少张这样的白纸?
要使粘合后的总长度为1006cm,需用多少张这样的白纸?
【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.

(1)根据题意,将下面的表格补充完整.
白纸张数x(张) | 1 | 2 | 3 | 4 | 5 | … |
纸条总长度y(cm) | 20 | 54 | 71 | … |
(2)直接写出y与x的关系式.
(3)要使粘合后的长方形总面积为1656cm2,则需用多少张这样的白纸?