题目内容
20.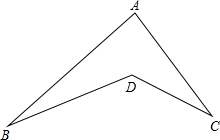 如图.点A、B、C、D是平面内四个点.连接AB、AC、BD、CD.
如图.点A、B、C、D是平面内四个点.连接AB、AC、BD、CD.(1)求证:∠BDC=∠A+∠B+∠C;
(2)如果点D与点A分别在线段BC的两侧.先画出图形.再猜想∠BDC、∠A、∠ABD、∠ACD这4个角之间有怎样的关系.并证明你的结论.
分析 (1)连结AD并延长,如图1,根据三角形外角性质得∠2=∠1+∠B,∠4=∠3+∠C,然后把两式相加即可得到结论;
(2)如图2,连结BC,根据三角形内角和定理得到∠1+∠2+∠A=180°,∠3+∠4+∠D=180°,然后把两式相加即可得∠BDC+∠A+∠ABD+∠ACD=360°.
解答 (1)证明:连结AD并延长,如图1,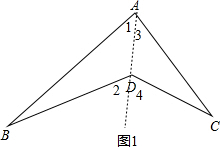
∵∠2=∠1+∠B,∠4=∠3+∠C,
∴∠2+∠4=∠1+∠B+∠3+∠C,
∴∠BDC=∠A+∠B+∠C;
(2)解:∠BDC+∠A+∠ABD+∠ACD=360°.理由如下:
如图2,连结BC,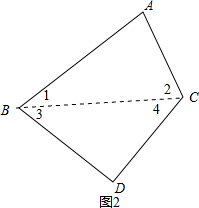
∵∠1+∠2+∠A=180°,∠3+∠4+∠D=180°,
∴∠1+∠2+∠A+∠3+∠4+∠D=360°,
∴∠BDC+∠A+∠ABD+∠ACD=360°.
点评 本题考查了三角形内角和定理:三角形内角和是180°.利用三角形内角和可直接根据两已知角求第三个角或依据三角形中角的关系,用代数方法求三个角,也可在直角三角形中,已知一锐角可利用两锐角互余求另一锐角.也考查了三角形外角性质.

练习册系列答案
相关题目
12.在抛物线y=ax2+bx+c上,部分点的横坐标x,纵坐标y的对应值如下表:
从上表可知,下列说法正确的有( )个
①抛物线与x轴的交点为(-2,0)(2,0);
②抛物线与y轴的交点为(0,6);
③在对称轴右侧,y随x增大而减少;
④抛物线的对称轴是:直线x=$\frac{1}{2}$.
| x | … | -3 | -2 | 0 | 1 | … |
| y | … | -6 | 0 | 6 | 6 | … |
①抛物线与x轴的交点为(-2,0)(2,0);
②抛物线与y轴的交点为(0,6);
③在对称轴右侧,y随x增大而减少;
④抛物线的对称轴是:直线x=$\frac{1}{2}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.若点P(m,2)与点Q(5,n)关于原点对称,则m、n的值分别是( )
| A. | -5,2 | B. | 5,-2 | C. | 5,2 | D. | -5,-2 |
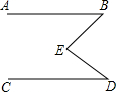 如图.已知AB∥CD,∠B=58°,∠D=40°,求∠BED的度数.(至少用两种方法求解)
如图.已知AB∥CD,∠B=58°,∠D=40°,求∠BED的度数.(至少用两种方法求解)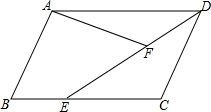 如图,在平行四边形ABCD中,已知E是BC上异于B、C的一点,∠AFE=∠B,AD=10,DC=6,AF=3,求DE.
如图,在平行四边形ABCD中,已知E是BC上异于B、C的一点,∠AFE=∠B,AD=10,DC=6,AF=3,求DE.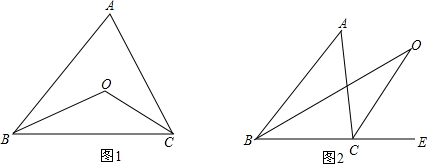
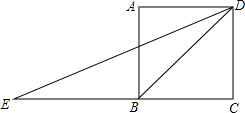 如图,正方形ABCD的边长为1,延长边CB到点E,使BE=BD.连接DE,∠CDE的度数是多少?
如图,正方形ABCD的边长为1,延长边CB到点E,使BE=BD.连接DE,∠CDE的度数是多少? 将边长为12cm的正方形铁片的四个角各剪去一个边长为3cm的小正方形,如图所示,剩余部分折成一个无盖的长方体盒子,该盒子的容积是108cm3.
将边长为12cm的正方形铁片的四个角各剪去一个边长为3cm的小正方形,如图所示,剩余部分折成一个无盖的长方体盒子,该盒子的容积是108cm3.