题目内容
已知x12+ax1+b=0，x22+ax2+b=0，则（x1+x2）（x12-x1x2+x22）=（ ）
| A、a3+ab |
| B、-a3+3ab |
| C、a3-3ab |
| D、-a3-ab |
考点：根与系数的关系
专题：
分析：根据完全平方公式，可转化成两根之和、两根之积的关系，再根据根与系数的关系，可得答案．
解答：解：由题意，得
x1，x2是关于x得一元二次方程x2+ax+b=0的两个根，
由根与系数的关系，得
x1+x2=-a，x1•x2=b．
则（x1+x2）（x12-x1x2+x22）
=（x1+x2）[（x1+x2）2-3x1x2]
=-a[（-a）2-3b]
=-a3+3ab．
故选：B．
x1，x2是关于x得一元二次方程x2+ax+b=0的两个根，
由根与系数的关系，得
x1+x2=-a，x1•x2=b．
则（x1+x2）（x12-x1x2+x22）
=（x1+x2）[（x1+x2）2-3x1x2]
=-a[（-a）2-3b]
=-a3+3ab．
故选：B．
点评：本题考查了根与系数的关系，利用了根与系数的关系．
练习册系列答案
相关题目
在一个钝角三角形中，如果一个三角形各边的长度都扩大3倍，那么这个三角形的两个锐角的余弦值（ ）
| A、都没有变化 |
| B、都扩大3倍 |
| C、都缩小为原来的3倍 |
| D、不能确定是否发生变化 |
如图，在Rt△ABC中，∠C=90°，CD⊥AB，BE平分∠ABC交CD于F，EH⊥CD于H，则下列结论错误的选项的是（ ）| A、AC2+BD2=BC2+AD2 | ||
B、CH=
| ||
C、
| ||
| D、若F为BE中点，则AD=3BD |
一个扇形的周长为8m，则它的最大面积是（ ）
| A、4m2 |
| B、6m2 |
| C、8m2 |
| D、10m2 |
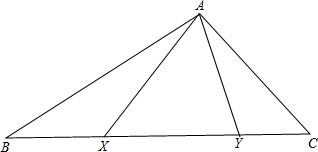如图，自△ABC的顶点A引两条射线交BC于X，Y，使得∠BAX=∠CAY，求证：