题目内容
6.下列分式是最简分式的是( )| A. | $\frac{1-x}{x-1}$ | B. | $\frac{{x}^{2}-1}{{x}^{2}+2x+1}$ | C. | $\frac{x-y}{{x}^{2}+{y}^{2}}$ | D. | -$\frac{13{m}^{2}}{2m}$ |
分析 要判断分式是否是最简分式,只需判断它能否化简,不能化简的即为最简分式.
解答 解:A、原式=-$\frac{1-x}{1-x}$=-1,不是最简分式,故本选项错误;
B、原式=$\frac{(x+1)(x-1)}{(x+1)^{2}}$=$\frac{x-1}{x+1}$,不是最简分式,故本选项错误;
C、该分式是最简分式,故本选项正确;
D、原式=-$\frac{13m}{2}$,不是最简分式,故本选项错误;
故选:C.
点评 此题考查了最简分式的判断,当分式的分子分母中除1以外再没有其他的公因式时,此时分式成为最简分式,一般情况下分式若不是最简分式,应将分子分母中的公因式约分后得到最简结果.掌握最简分式的判断方法是解本题的关键.

练习册系列答案
相关题目
16.下列各式计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$ | C. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{3}$ |
14.下列多项式中,能运用公式法进行因式分解的是( )
| A. | a2+b2 | B. | x2+9 | C. | m2-n2 | D. | x2+2xy+4y2 |
15.计算2-2的结果是( )
| A. | -4 | B. | 4 | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |

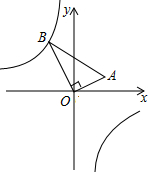 如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2$\sqrt{5}$,反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值为-8.
如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2$\sqrt{5}$,反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值为-8. 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A,B,C在小正方形的顶点上.以点O为坐标原点建立平面直角坐标系,请回答下列问题:
如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A,B,C在小正方形的顶点上.以点O为坐标原点建立平面直角坐标系,请回答下列问题: