题目内容
【题目】在平面直角坐标系
中，作抛物线
关于
轴对称的抛物线
，再将抛物线向左平移2个单位，向上平移1个单位，得到的抛物线
的函数解析式是
，则抛物线所对应的的函数解析式是( )
A.
B.
C.
D.
【答案】D
【解析】
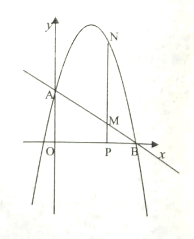
易得抛物线C的顶点，进而可得抛物线B的顶点坐标，根据顶点式及平移前后二次项系数不变可得抛物线B的解析式，而根据关于x轴对称的两条抛物线的顶点的横坐标相等，纵坐标互为相反数，二次项系数互为相反数可得抛物线A所对应的的函数表达式
易得抛物线C的顶点（-1，-1），
∵是向左平移2个单位，向上平移1个单位得到抛物线C，
∴抛物线B的顶点坐标（1，-2），
可设抛物线B的解析式为y=2
+k，代入得y=2
-2，
易得抛物线A的二次项系数为-2，顶点坐标为（1,2），
∴抛物线A的解析式为y=-2+2，
故正确答案为D.
练习册系列答案
相关题目
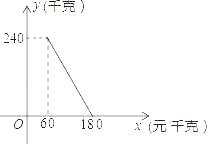
【题目】现有
、
型两种客车，它们的载客量和租金如下表：
|
| |
载客量/（人/辆） |
|
|
租金/（元/辆） |
|
|
某学校计划在总费用
元的限额内，租用、型客车共5辆送九年级师生集体外出活动.
（Ⅰ）设租用型客车
辆（为非负整数），根据题意，用含的式子填写下表：
车辆数/辆 | 载客量 | 租金/元 | |
|
|
|
|
|
|
（Ⅱ）若九年级师生共有
人，请给出能完成此项任务的最节省费用的租车方案，并说明理由.
