题目内容
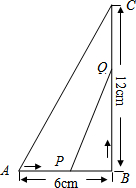 如图,在△ABC中,∠B=90°,点P从点A开始,沿AB向点B以1厘米/秒的速度移动,点Q从B点开始沿BC以2厘米/秒的速度移动,如果P、Q分别从A、B同时出发:
如图,在△ABC中,∠B=90°,点P从点A开始,沿AB向点B以1厘米/秒的速度移动,点Q从B点开始沿BC以2厘米/秒的速度移动,如果P、Q分别从A、B同时出发:(1)几秒后四边形APQC的面积是31平方厘米?
(2)若用S表示四边形APQC的面积,在经过多长时间S取得最小值?并求出最小值.
考点:一元二次方程的应用,二次函数的应用
专题:几何动点问题
分析:(1)设经过x秒钟,可使得四边形APQC的面积是31平方厘米,根据题意列出关于x的方程,求出方程的解即可得到结果;根据面积为31列出方程,判断即可得到结果.
(2)根据题意列出S关于x的函数关系式,利用函数的性质来求最值.
(2)根据题意列出S关于x的函数关系式,利用函数的性质来求最值.
解答: 解:(1)设经过x秒钟,可使得四边形APQC的面积是31平方厘米,
解:(1)设经过x秒钟,可使得四边形APQC的面积是31平方厘米,
根据题意得:
BP•BQ=
AB•BC-31,即
(6-x)•2x=
×6×12-31,
整理得 (x-1)(x-5)=0
解得:x1=1,x2=5.
答:经过1或5秒钟,可使得四边形APQC的面积是31平方厘米;
(2)依题意得,S四边形APQC=S△ABC-S△BPQ,即S=
AB•BC-
BP•BQ=
×6×12-
(6-x)•2x=(x-3)2+27(0<x<6),
当x-3=0,即x=3时,S最小=27.
答:经过3分钟时,S取得最小值27平方厘米.
 解:(1)设经过x秒钟,可使得四边形APQC的面积是31平方厘米,
解:(1)设经过x秒钟,可使得四边形APQC的面积是31平方厘米,根据题意得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
整理得 (x-1)(x-5)=0
解得:x1=1,x2=5.
答:经过1或5秒钟,可使得四边形APQC的面积是31平方厘米;
(2)依题意得,S四边形APQC=S△ABC-S△BPQ,即S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当x-3=0,即x=3时,S最小=27.
答:经过3分钟时,S取得最小值27平方厘米.
点评:此题考查了一元二次方程的应用、二次函数的性质,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若多项式2x3-8x2+x-1与3x3-2mx2-5x+3的和不含二次项,则m的值为( )
| A、2 | B、-2 | C、4 | D、-4 |
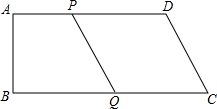 如图,梯形ABCD中,AD∥BC,AB⊥BC,点P从A出发以1厘米/秒的速度沿AD移动,点Q同时从C出发以2厘米/秒的速度沿CB移动,若AD=18厘米,BC=24厘米.求:
如图,梯形ABCD中,AD∥BC,AB⊥BC,点P从A出发以1厘米/秒的速度沿AD移动,点Q同时从C出发以2厘米/秒的速度沿CB移动,若AD=18厘米,BC=24厘米.求: 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第
小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第