题目内容
小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的哪一块带去，就能配一块与原来一样大小的三角形？应该带第考点：全等三角形的应用
专题：
分析：本题应先假定选择哪块，再对应三角形全等判定的条件进行验证．
解答：解：1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素，所以不能带它们去，
只有第2块有完整的两角及夹边，符合ASA，满足题目要求的条件，是符合题意的．
故答案为：2．
只有第2块有完整的两角及夹边，符合ASA，满足题目要求的条件，是符合题意的．
故答案为：2．
点评：本题主要考查三角形全等的判定，看这4块玻璃中哪个包含的条件符合某个判定．判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
练习册系列答案
名校课堂系列答案
相关题目
下列叙述正确的是（ ）
| A、正数和分数统称有理数 | ||
| B、0是整数但不是正数 | ||
C、-
| ||
| D、既不是正数，又不是负数，这样的数一定不是有理数 |
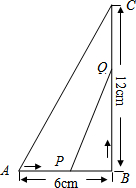如图，在△ABC中，∠B=90°，点P从点A开始，沿AB向点B以1厘米/秒的速度移动，点Q从B点开始沿BC以2厘米/秒的速度移动，如果P、Q分别从A、B同时出发：