题目内容
如图,△ABC中,AB>AC,D为AB上一点,下列条件:①∠B=∠ACD,②∠ADC=∠ACB,③ ,④
,④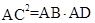 中,能判定△ABC与△ACD相似的有( )
中,能判定△ABC与△ACD相似的有( )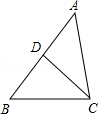
| A.1个 | B.2个 | C.3个 | D.4个 |
C.
解析试题分析: ∵∠A是公共角,
∴当∠B=∠ACD时,△ABC∽△ACD(有两组角对应相等的两个三角形相似);
当∠ADC=∠ACB,△ABC∽△ACD(有两组角对应相等的两个三角形相似);
当 时,∠A不是夹角,则不能判定△ABC与△ACD相似;
时,∠A不是夹角,则不能判定△ABC与△ACD相似;
当AC2=AD•AB时,即 ,△ABC∽△ACD(两组对应边的比相等且夹角对应相等的两个三角形相似).
,△ABC∽△ACD(两组对应边的比相等且夹角对应相等的两个三角形相似).
∴能够判定△ABC与△ACD相似的条件有三个:①②④.故选C.
考点:相似三角形的判定.

练习册系列答案
相关题目
已知,AB是⊙O的直径,且C是圆上一点,小聪透过平举的放大镜从正上方看到水平桌面上的三角形图案的∠B(如图所示),那么下列关于∠A与放大镜中的∠B关系描述正确的是( )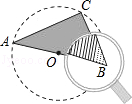
| A.∠A+∠B=900 | B.∠A=∠B |
| C.∠A+∠B>900 | D.∠A+∠B的值无法确定 |
如图2,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式: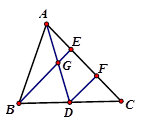
①AG:AD=1:2; ②GE:BE=1:3 ③BE:BG=4:3,
其中正确的是( )
| A.①② | B.①③ | C.②③ | D.①②③ |
小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )
| A.10米 | B.12米 | C.15米 | D.22.5米 |
若 ,且
,且 ,则
,则 的值是( )
的值是( )
| A.14 | B.42 | C.7 | D.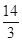 |

 ,则△EFC的周长为( )
,则△EFC的周长为( )
 ; ④AC2=AD·AB.其中单独能够判定△ABC∽△ACD的有( )
; ④AC2=AD·AB.其中单独能够判定△ABC∽△ACD的有( )




