题目内容
10．
如图，在钝角三角形ABC中，CB=9，AB=17，AC=10，AD⊥BC，垂足为D，求CD的长．
分析 设AD=x，BD=y，在直角△ADB中，根据勾股定理得AB2=x2+y2，在直角△ADC中，由勾股定理得到方程AC2=x2+（y-BC）2，解方程即可得到结果．
解答 解：设AD=x，BD=y，
∵在直角△ADB中，AB2=x2+y2，即172=x2+y2，
在直角△ADC中，AC2=x2+（y-BC）2，即102=x2+（y-9）2，
解方程得 y=15，
∴CD=BD-BC=15-9=6．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
口算能手系列答案
相关题目
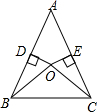如图，在△ABC中，点O是△ABC内的一点，联结OB、OC，点D、E分别是边AB、AC的中点，且OD⊥AB，OE⊥AC，OC=5，求OB的长．
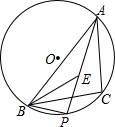如图，已知BC是⊙O的一条弦，点A是⊙0的优弧BC上的一个动点（点A与B，C不重合），∠BAC的平分线AP交⊙O于点P．∠ABC的平分线BE交AP于点E，连结BP．