Question

18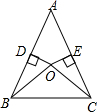．如图，在△ABC中，点O是△ABC内的一点，联结OB、OC，点D、E分别是边AB、AC的中点，且OD⊥AB，OE⊥AC，OC=5，求OB的长．

Answer 1

分析 首先连接AO，进而可得DO是AB的垂直平分线，OE是AC的垂直平分线，根据线段垂直平分线的性质可得AO=BO=CO，进而可得答案．

解答 解：连接AO，
∵点D是边AB的中点，且OD⊥AB，
∴DO是AB的垂直平分线，
∴BO=AO，
∵点E分别是边AC的中点，且OE⊥AC，
∴OE是AC的垂直平分线，
∴AO=CO，
∴BO=CO=5．

点评 此题主要考查了线段垂直平分线的性质，关键是掌握线段垂直平分线上任意一点，到线段两端点的距离相等．