题目内容
18.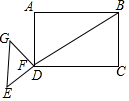 已知,如图,在矩形ABCD中,AD=4,AB=8,等腰△EFG,EG=FG=3,EF=$\frac{6\sqrt{5}}{5}$,点D与点F重合,将△EFG绕点D顺时针旋转α(0°<α<90°),在旋转过程中,设直线EG分别与BA、射BD相交于M、N,当△BMN是以∠ABD为底角的等腰三角形时,线段BM=$\frac{13}{2}$.
已知,如图,在矩形ABCD中,AD=4,AB=8,等腰△EFG,EG=FG=3,EF=$\frac{6\sqrt{5}}{5}$,点D与点F重合,将△EFG绕点D顺时针旋转α(0°<α<90°),在旋转过程中,设直线EG分别与BA、射BD相交于M、N,当△BMN是以∠ABD为底角的等腰三角形时,线段BM=$\frac{13}{2}$.
分析 如图,作DR⊥EG于R,GH⊥DE于H,作MP⊥BD于P.思想利用勾股定理求出GH,再根据$\frac{1}{2}$•DE•GH=$\frac{1}{2}$•EG•DR,求出DR,由sin∠DNR=sin∠ABD=$\frac{DG}{DN}$=$\frac{\sqrt{5}}{5}$,
推出DN=$\frac{6\sqrt{5}}{5}$,推出BN=DN+BD=$\frac{26\sqrt{5}}{5}$,由MN=MB,MP⊥BN,推出BP=ON=$\frac{13\sqrt{5}}{5}$,由cos∠PBM=$\frac{PB}{BM}$=$\frac{2\sqrt{5}}{5}$,即可解决问题.
解答 解:如图,作DR⊥EG于R,GH⊥DE于H,作MP⊥BD于P.
∵∠MNB=∠MBN,
∴MN=MB,
∵GE=GF=3,GH⊥EF,
∴EH=HF=$\frac{3}{5}$$\sqrt{5}$,
∴GH=$\sqrt{E{G}^{2}-E{H}^{2}}$=$\sqrt{{3}^{2}-(\frac{3\sqrt{5}}{5})^{2}}$=$\frac{6\sqrt{5}}{5}$,
∵$\frac{1}{2}$•DE•GH=$\frac{1}{2}$•EG•DR,
∴DR=$\frac{DE•GH}{EG}$=$\frac{\frac{3\sqrt{5}}{5}•\frac{6\sqrt{5}}{5}}{3}$=$\frac{6}{5}$,
在Rt△ABD中,BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
由sin∠DNR=sin∠ABD=$\frac{DG}{DN}$=$\frac{\sqrt{5}}{5}$,
∴DN=$\frac{6\sqrt{5}}{5}$,
∴BN=DN+BD=$\frac{26\sqrt{5}}{5}$,
∵MN=MB,MP⊥BN,
∴BP=ON=$\frac{13\sqrt{5}}{5}$,
由cos∠PBM=$\frac{PB}{BM}$=$\frac{2\sqrt{5}}{5}$,
∴BM=$\frac{13}{2}$.
点评 本题考查旋转变换、矩形的性质、解直角三角形、锐角三角函数、勾股定理等知识,解题的关键是学会添加常用辅助线,学会利用面积法求线段的长,属于中考填空题中的压轴题.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案| A. | -1<x0<0 | B. | 0<x0<1 | C. | 1<x0<2 | D. | 2<x0<3 |
 如图,等边三角形ABC中,D为AC上一点,E为AB延长线上一点,DE⊥AC交BC于点F,且DF=EF.
如图,等边三角形ABC中,D为AC上一点,E为AB延长线上一点,DE⊥AC交BC于点F,且DF=EF.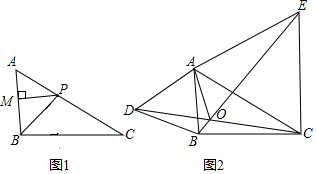
 已知:如图,在△ABC中,AB=AC,BD=CD,DE⊥AB于E,DF⊥AC于F.求证:DE=DF.
已知:如图,在△ABC中,AB=AC,BD=CD,DE⊥AB于E,DF⊥AC于F.求证:DE=DF.