题目内容
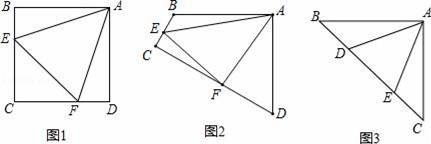
如图,△ABC中∠CAB的平分线AD和边BC的垂直平分线ED相交于点D,过点D作DF垂直于AC交AC的延长线于点F,作DM垂直于AB交AB于点M.
 (1)猜想CF和BM之间有何关系,并说明理由;
(1)猜想CF和BM之间有何关系,并说明理由;
(2)求证:AB-AC=2CF
(1)CF=BM.理由:连接CD,DB,
∵AD平分∠CAB,DF⊥AC,DM⊥AB, ∴DF=DM.
∵DE垂直平分BC,
∴CD=BD.
 ∵∠AFD=∠DMB=90°,
∵∠AFD=∠DMB=90°,
∴Rt△CDF≌Rt△BDM.
∴CF=BM.
(2)证明: ∵AD=AD,DF=DM,∠AFD=∠AMD=90° ,
,
∴Rt△AFD≌Rt△AMD,
 ∴AF=AM.
∴AF=AM.
∵AB=AM+BM,AF=AC+CF,AF=AM,BM=CF,
∴AB=AC+2CF.
∴AB-AC=2CF.

练习册系列答案
相关题目
 ,化简
,化简 +|a﹣2|的结果是( )
+|a﹣2|的结果是( )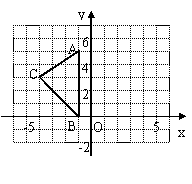
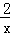 ,下列说法正确的是( )
,下列说法正确的是( )
 方形ABOC的边长是2,反比例函数y=
方形ABOC的边长是2,反比例函数y=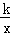 (x≠0)图象经过点A,则k的值是( )
(x≠0)图象经过点A,则k的值是( )