题目内容
12．
如图，△ABC三个内角的平分线交于点O，点D在CA的延长线上，且DC=BC，若∠D=20°，则∠ABC的度数为40°．
分析 由条件可证明△DOC≌△BOC，则可求得∠OBC，再由角平分线的定义可求得∠ABC的度数．
解答 解：
∵OC平分∠BCA，
∴∠DCO=∠BCO，
在△DOC和△BOC中
$\left\{\begin{array}{l}{DC=BC}\\{∠DCO=∠BCO}\\{OC=OC}\end{array}\right.$
∴△DOC≌△BOC（SAS），
∴∠CBO=∠D=20°，
∵OB平分∠ABC，
∴∠ABC=2∠CBO=40°，
故答案为：40°．
点评 本题主要考查全等三角形的判定和性质，掌握全等三角形的判定方法（即SSS、SAS、ASA、AAS和HL）和全等三角形的性质（对应角相等、对应边相等）是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
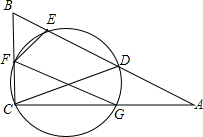如图，D为Rt△ABC斜边AB上一点，以CD为直径的圆分别交△ABC三边于E、F、G三点，连接FE，FG．
