Question

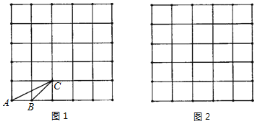
【题目】如图，平面直角坐标系中，△ABC为等边三角形，其中点A，B，C的坐标分别为(－3，－1)，(－3，－3)，(－3＋，－2)．现以y轴为对称轴作△ABC的对称图形，得△A1B1C1，再以x轴为对称轴作△A1B1C1的对称图形，得△A2B2C2.

(1)直接写出点C1，C2的坐标．

(2)能否通过一次旋转将△ABC旋转到△A2B2C2的位置？若能，请直接写出所旋转的度数；若不能，请说明理由．

(3)设当△ABC的位置发生变化时，△A2B2C2，△A1B1C1与△ABC之间的对称关系始终保持不变．

①当△ABC向上平移多少个单位长度时，△A1B1C1与△A2B2C2完全重合？并直接写出此时点C的坐标；

②将△ABC绕点A顺时针旋转α°(0≤α≤180)，使△A1B1C1与△A2B2C2完全重合，此时α的值为多少？点C的坐标又是什么？

Answer 1

【答案】（1）点C1，C2的坐标分别为(3－，－2)，(3－，2)；（2）能，旋转的度数为180°；（3）①当△ABC向上平移2个单位长度，C的坐标为(－3＋，0)；②当α＝180时，△A1B1C1与△A2B2C2完全重合，此时点C的坐标为(－3－，0)

【解析】

（1）根据关于坐标轴对称点的坐标的特点即可解答；（2）观察图象，根据旋转的性质可知：旋转的度数为180°能通过一次旋转将△ABC旋转到△A2B2C2的位置；（3）①根据图形和平移的性质可知：当△ABC向上平移2个单位时，△A1B1C1与△A2B2C2完全重合，此时点C的坐标为（-3+ ，0）；②利用旋转的性质可知：当α=180时，△A1B1C1与△A2B2C2完全重合，此时点C的坐标为（-3-，0）．

(1)点C1，C2的坐标分别为(3－，－2)，(3－，2)．

(2)能通过一次旋转将△ABC旋转到△A2B2C2的位置，所旋转的度数为180°.

(3)①当△ABC向上平移2个单位长度时，△A1B1C1与△A2B2C2完全重合，此时点C的坐标为(－3＋，0)(如图1)；

②当α＝180时，△A1B1C1与△A2B2C2完全重合，此时点C的坐标为(－3－，0)(如图2)．