题目内容
如图，矩形ABCD中，CF⊥BD于F，点E恰好是AD的中点，AD=4，则CD的长为考点：矩形的性质
专题：
分析：根据矩形的性质和条件可证明△BCD∽△CDE，再利用相似三角形的性质可求得CD．
解答：解：∵四边形ABCD为矩形，
∴BC=AD=4，∠EDC=∠BCD=90°，
∵CF⊥BD，
∴∠EDF+∠BDC=∠DEF+∠EDF=90°，
∴∠DEF=∠BDC，
∴△BCD∽△CDE，
∴
=
，
又E为AD中点，
∴DE=2，
∴
=
，
解得CD=2
，
故答案为：2
．
∴BC=AD=4，∠EDC=∠BCD=90°，
∵CF⊥BD，
∴∠EDF+∠BDC=∠DEF+∠EDF=90°，
∴∠DEF=∠BDC，
∴△BCD∽△CDE，
∴
| CD |
| DE |
| BC |
| CD |
又E为AD中点，
∴DE=2，
∴
| CD |
| 2 |
| 4 |
| CD |
解得CD=2
| 2 |
故答案为：2
| 2 |
点评：本题主要考查矩形的性质和相似三角形的判定和性质，根据条件证明△BCD∽△CDE是解题的关键．
练习册系列答案
相关题目
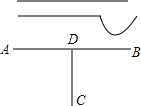水质卫生状况关系到千家万户，是重大民生工程，泗阳县城乡供水一体化模式的实践被群众称为“德政工程”、“惠民工程”．如图，2014年计划把大运河（AB）中的水引到水厂C中，可先过C作CD⊥AB，垂足为D，然后沿CD开渠，则能使所开的渠道最短，这种设计方案的根据是
如图，已知线段AB的两个端点在直角坐标系中的坐标分别是A（m，m），B（2n，n），以原点O为位似中心，相似比为