题目内容
18.方程3x+2y=17的正整数解有( )| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
分析 把方程化为用一个未知数表示成另一个未知数的形式,再根据x、y均为正整数求解即可.
解答 解:
方程2x+3y=17可化为x=$\frac{17-2y}{3}$,
∵x、y均为正整数,
∴17-2y>0且为3的倍数,
当y=1时,x=5,
当y=4时,x=3,
当y=7时,x=1,
∴方程3x+2y=17的正整数解为$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$,$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$,$\left\{\begin{array}{l}{x=1}\\{y=7}\end{array}\right.$,
故选:C.
点评 本题主要考查方程的特殊解,用一个未知数表示成另一个未知数是解题的关键.

练习册系列答案
相关题目
8.某数学兴趣小组利用假期50天社会实践参与了一家网店经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如表所示.
(1)设销售该新型商品的当天利润为y元,当1≤x<30时,
①求出y与x的函数关系式;
②问销售该商品第几天时,当天利润最大,最大利润是多少?
(2)该商品在销售过程中,第1天至第30天当天利润不低于1200元?$(\sqrt{3}≈1.73)$.
| 时间第x(天) | 1≤x<30 | 30≤x≤50 |
| 售价(元/件) | x+30 | 60 |
| 每天销量(件) | 100-2x | |
①求出y与x的函数关系式;
②问销售该商品第几天时,当天利润最大,最大利润是多少?
(2)该商品在销售过程中,第1天至第30天当天利润不低于1200元?$(\sqrt{3}≈1.73)$.
6.下列计算正确的是( )
| A. | a3-a2=a | B. | a2•a3=a6 | C. | (a-b)2=a2-b2 | D. | (-a2)3=-a6 |
8.吉州区为推动教育优质均衡发展,发挥教育公平的基础性作用,近几年来共投入了教育经费10亿元,用科学记数法表示10亿为( )
| A. | 10×108 | B. | 0.1×1010 | C. | 1×109 | D. | 1×1010 |
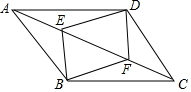 已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:EB∥DF.
已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:EB∥DF.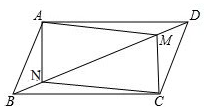 如图,BD是?ABCD的一条对角线,且△ABN与△ADM的面积相等.
如图,BD是?ABCD的一条对角线,且△ABN与△ADM的面积相等.